로딩 중이에요... 🐣
27 데이터분석 및 시각화 기술통계및 데이터 분포확인 | ✅ 저자: 이유정(박사)
기술통계란?
기술통계는 데이터를 요약하고 설명하기 위한 통계입니다.
데이터의 중심, 퍼짐 정도, 모양 등을 파악하는 데 사용합니다.
예시로 설명하면:
"학생 100명의 시험 점수"가 있다면,
전체 평균 점수는 몇 점인지?
누가 평균에서 많이 벗어났는지?
점수가 어느 쪽으로 치우쳤는지?
이런 걸 알려주는 것이 기술통계입니다.
✅ 1. 중심 경향 (중간값, 평균 등)
데이터를 대표하는 값을 말해요.
예: 시험 점수, 월급, 키, 몸무게의 평균
| 구분 | 설명 | 예시 | Pandas 코드 |
|---|---|---|---|
| 평균 (mean) | 모든 값을 더해서 개수로 나눈 값 | 평균 키, 평균 점수 | df['height'].mean() |
| 중앙값 (median) | 크기 순으로 나열했을 때 중간에 있는 값 | 중간 성적 | df['height'].median() |
| 최빈값 (mode) | 가장 많이 나온 값 | 가장 많이 받은 점수 | df['height'].mode() |
import pandas as pd
# 학생들의 키 데이터 예시
data = {
'height': [160, 162, 163, 160, 165, 170, 160]
}
df = pd.DataFrame(data)
# 평균
mean_val = df['height'].mean()
print("평균:", mean_val) # 모든 키의 합을 개수로 나눈 값
# 중앙값
median_val = df['height'].median()
print("중앙값:", median_val) # 크기순 정렬 후 중간 값
# 최빈값
mode_val = df['height'].mode()
print("최빈값:", mode_val[0]) # 가장 많이 나온 값
출력결과:
평균: 163.42857142857142
중앙값: 162
최빈값: 160
✅ 2. 퍼짐 정도 (분산과 표준편차)
데이터가 얼마나 퍼져 있는지, 즉 다들 비슷한 값인지, 차이가 큰지를 알려줘요.
- 예시:
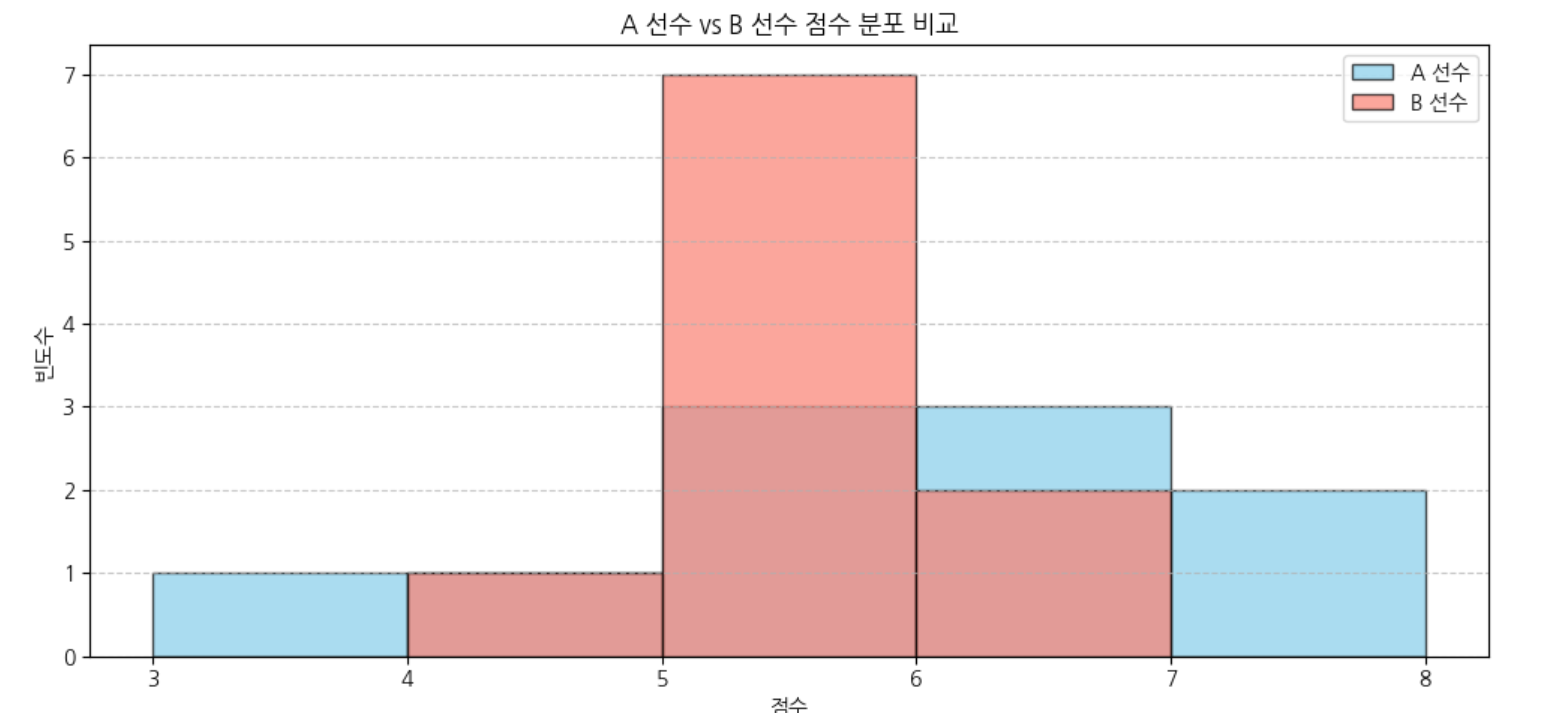
A선수는 공을 항상 5~6m 정도로 일정하게 던져요.
B선수는 공을 어떨 땐 4m, 어떨 땐 7m 이상 던져요.
이렇게 던진 거리의 차이가 클수록, B선수처럼 표준편차가 크다고 해요.
반대로 항상 비슷한 거리로 던지면, A선수처럼 표준편차가 작다고 해요.
분산과 편차 그래프

| 용어 | 설명 | Pandas 코드 |
|---|---|---|
| 분산 (Variance) | 평균에서 얼마나 떨어져 있는지를 계산 | df['score'].var() |
| 표준편차 (Std Dev) | 분산을 루트 씌운 것 (더 직관적 수치) | df['score'].std() |
pandas로 분산 var( )과 표준편차 std( ) 구하기:
import pandas as pd
import matplotlib
print(matplotlib.get_configdir())
# A선수와 B선수의 점수 데이터
scores = {
"A": [5, 6, 7, 4, 6, 5, 3, 7, 6, 5],
"B": [5, 5, 6, 5, 4, 5, 5, 5, 6, 5]
}
# 데이터프레임 생성
df = pd.DataFrame(scores)
# 평균
print("평균:")
print(df.mean())
# 분산 (Variance)
print("\n분산:")
print(df.var(ddof=0)) # 모집단 분산 (SQL과 동일하게 ddof=0)
# 표준편차 (Standard Deviation)
print("\n표준편차:")
print(df.std(ddof=0)) # 모집단 표준편차
출력결과:
평균:
A 5.4
B 5.1
dtype: float64 # 64비트 실수형
분산:
A 1.44
B 0.29
dtype: float64 # 64비트 실수형
표준편차:
A 1.200000
B 0.538516
dtype: float64 # 64비트 실수형
Jupyter Notebook을 새로 열어도, 매번 plt.rc()를 쓰지 않고도
자동으로 한글 폰트가 적용되게 만드는 방법
import matplotlib
print(matplotlib.get_configdir())
예상출력:
/home/your_root/.config/matplotlib
이면, 설정 파일은 해당 폴더에 있어야 합니다.
matplotlibrc 파일 만들기 (없다면)
!mkdir -p ~/.config/matplotlib # 디렉토리 없으면 생성
!touch ~/.config/matplotlib/matplotlibrc # 설정 파일 생성
Jupyter Notebook에서는 cd, touch 대신 !을 붙여 사용합니다.
upyter에서는 직접 파일을 열 수 없으니 아래 코드로 내용을 씁니다:
config_text = """
font.family: NanumGothic
axes.unicode_minus: False
"""
with open(f"{matplotlib.get_configdir()}/matplotlibrc", "w", encoding="utf-8") as f:
f.write(config_text)
폰트 설치 (이미 설치했으니 생략) 만약 한글 폰트가 설치되지 않았다면 vscode에서 폰트 설치를 해야 합니다.
sudo apt-get install -y fonts-nanum
캐시 삭제 (중요!)
import matplotlib
import os
font_cache = os.path.join(matplotlib.get_cachedir(), 'fontlist-v330.json') # 버전에 따라 다를 수 있음
if os.path.exists(font_cache):
os.remove(font_cache)
print("폰트 캐시 삭제 완료! Jupyter를 완전히 재시작하세요.")
else:
print("캐시 파일이 이미 없거나, 경로가 다를 수 있습니다.")
Jupyter 완전히 재시작
- 브라우저에서 Jupyter 탭 닫기
터미널에서 Jupyter 서버 종료- 다시 실행하면 폰트 설정이 적용됨
✅ 3. 왜도와 첨도 (데이터의 "모양")
🔹왜도 (Skewness) 데이터가 평균을 중심으로 얼마나 비대칭인지, 어느 한쪽으로 치우쳐 있는지를 숫자로 알려주는 지표입니다. - 예: - 왼쪽으로 치우침: 대부분 점수가 높은 경우 - 오른쪽으로 치우침: 대부분 점수가 낮은 경우
df['score'].skew()
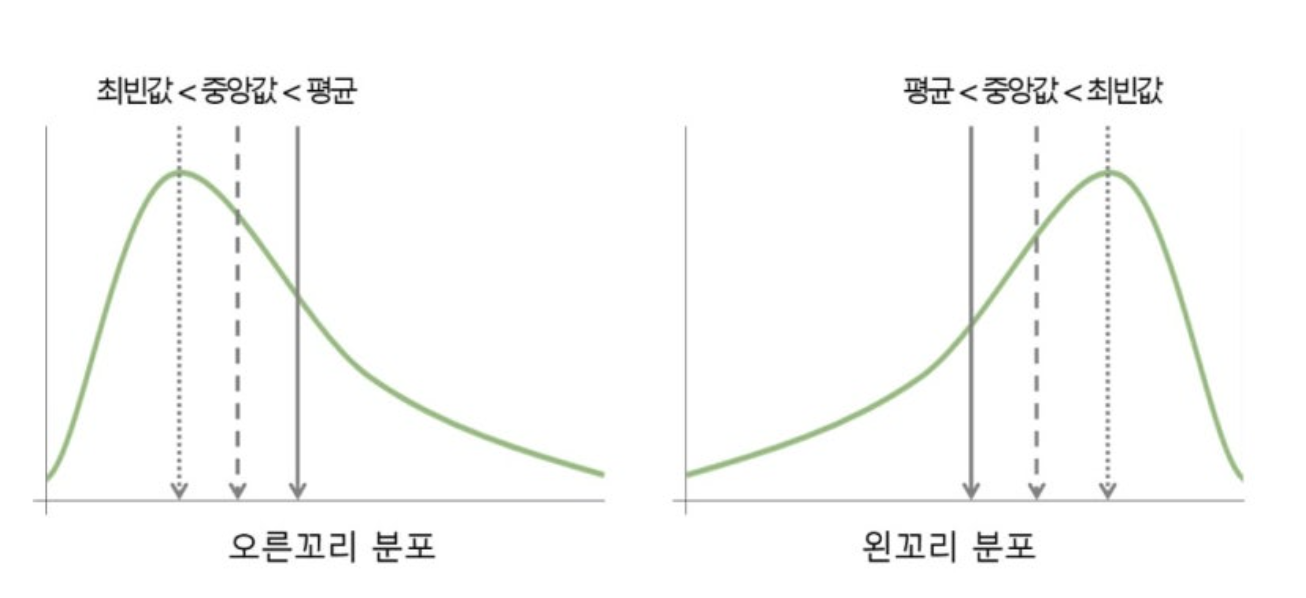
데이터가 평균을 중심으로 균형 있게 퍼져 있는지,
아니면 한쪽으로 치우쳐 있는지를 알아보기 위한 그래프입니다.
 왜 이것이 중요한가?
왜 이것이 중요한가?
-
평균만으로는 부족하기 때문이에요.
- 평균이 같아도 데이터가 좌우로 얼마나 퍼져 있는지는 다를 수 있어요.
- 예를 들어 평균 점수가 70점이라도:
- 어떤 반은 대부분이 70점 주변
- 어떤 반은 어떤 학생은 30점, 어떤 학생은 100점
-
데이터가 한쪽에 쏠려 있다면 해석이 달라집니다.
- 오른쪽으로 치우친 분포: 대부분 낮은 값, 일부 예외적으로 큰 값
- 왼쪽으로 치우친 분포: 대부분 높은 값, 일부 예외적으로 낮은 값
-
적절한 분석 방법을 선택하는 데 도움이 됩니다.
- 정규분포(균형 잡힌 분포)를 가정하는 통계 기법은 왜도에 민감해요.
- 왜도가 크면, 평균 대신 중앙값을 쓰거나, 데이터를 변환(log 등) 해야 할 수도 있어요.
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
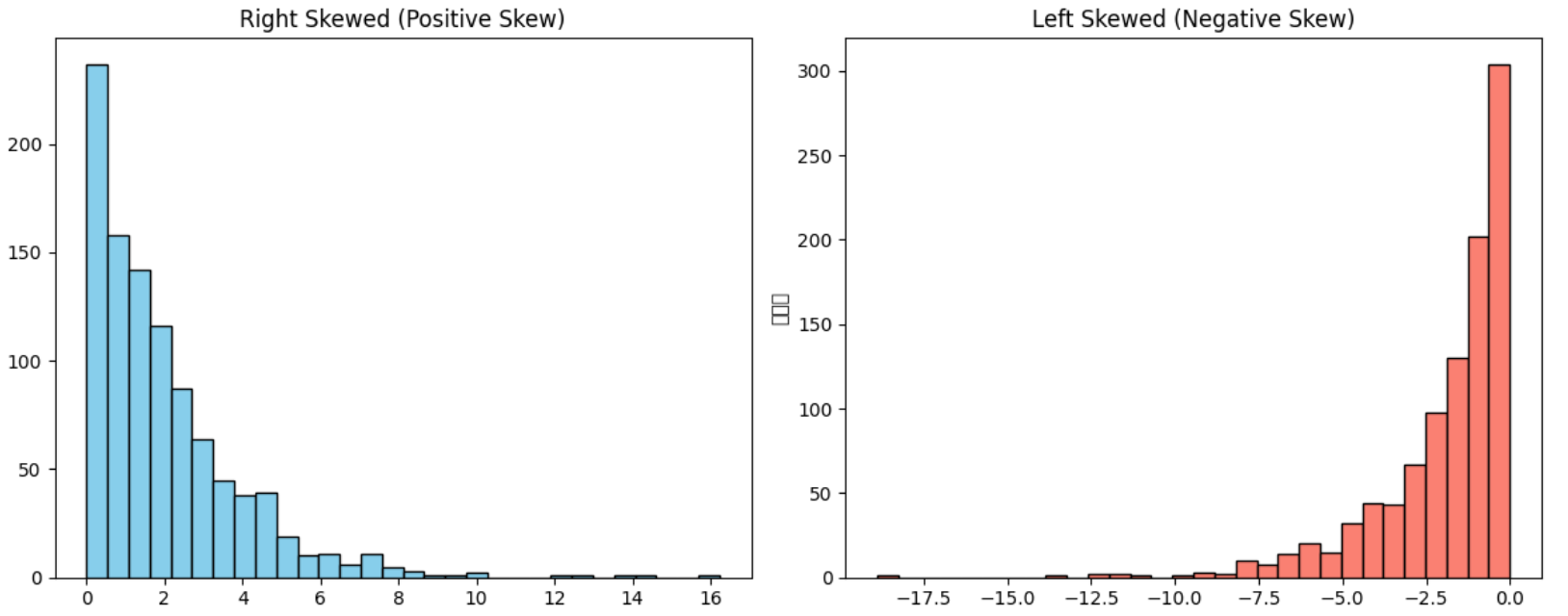
# 예제 1: 오른쪽으로 치우친 분포 (양의 왜도)
right_skewed = np.random.exponential(scale=2, size=1000)
# 예제 2: 왼쪽으로 치우친 분포 (음의 왜도)
left_skewed = -1 * np.random.exponential(scale=2, size=1000)
# 판다스 시리즈로 변환
df = pd.DataFrame({
'Right_Skewed': right_skewed,
'Left_Skewed': left_skewed
})
# 왜도 계산
print("왜도 (Skewness)")
print(df.skew())
print("\n양의 왜도: 평균 > 중앙값 > 최빈값")
print("음의 왜도: 평균 < 중앙값 < 최빈값")
# 시각화
plt.figure(figsize=(12, 5))
plt.subplot(1, 2, 1)
plt.hist(df['Right_Skewed'], bins=30, color='skyblue', edgecolor='black')
plt.title('Right Skewed (Positive Skew)')
plt.xlabel('값')
plt.ylabel('빈도수')
plt.subplot(1, 2, 2)
plt.hist(df['Left_Skewed'], bins=30, color='salmon', edgecolor='black')
plt.title('Left Skewed (Negative Skew)')
plt.xlabel('값')
plt.ylabel('빈도수')
plt.tight_layout()
plt.show()
출력결과:
왜도 (Skewness)
Right_Skewed 2.148461
Left_Skewed -2.228526
dtype: float64
양의 왜도: 평균 > 중앙값 > 최빈값
음의 왜도: 평균 < 중앙값 < 최빈값
🔹첨도 (Kurtosis) 첨도는 분포의 "뾰족함" 또는 "평평함"을 나타내는 통계 지표예요. - 뾰족하면: 대부분 비슷한 값이라고 판단하며 - 평평하면: 다양한 값이 섞여 있음을 의미합니다.
쉽게 이해하기:
-
어떤 시험에서 모두가 비슷한 점수(예: 80점)를 받았다면?
→ 그래프가 뾰족하게 솟아 있어요 → 첨도가 높다라고 합니다. -
어떤 시험에서 점수가 다양하게 퍼져 있다면(예: 20점~100점)?
→ 그래프가 낮고 평평하게 퍼져 있어요 → 첨도가 낮다라고 합니다.
df['score'].kurt()
실제 예시로 정리 예를 들어, 아래와 같은 시험 점수가 있다고 가정해볼게요.
import pandas as pd
df = pd.DataFrame({
'score': [50, 60, 70, 80, 90, 100, 100, 100]
})
- 평균 점수:
df['score'].mean()→ 81.25점 - 가장 많은 점수:
df['score'].mode()→ 100점 - 중간 점수:
df['score'].median()→ 85점 - 점수 퍼짐 정도:
df['score'].std()→ 약 18.53 - 점수 치우침(왜도):
df['score'].skew()→ 음수면 왼쪽 치우침 - 점수 집중도(첨도):
df['score'].kurt()→ 양수면 뾰족함
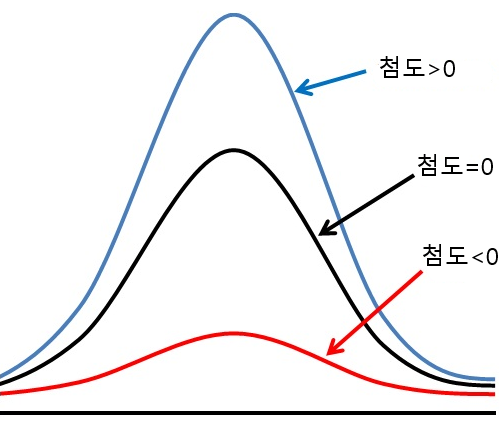
첨도의 기준 (기본적으로는 정규분포 대비)
| 첨도 값 . | 분포 형태 | 설명 |
|---|---|---|
| 0 | 정규분포 | 기준점. 평균적인 뾰족함 (보통의 종 모양 분포) |
| > 0 | 뾰족한 분포 (레프토쿠르틱, leptokurtic) | 중심값 주변에 데이터가 몰림. 극단값(outlier)이 많을 수 있음 |
| < 0 | 평평한 분포 (플라티쿠르틱, platykurtic) | 값이 넓게 퍼짐. 극단값이 적고 전체적으로 균일하게 분포됨 |
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 점수 데이터
df = pd.DataFrame({
'score': [50, 60, 70, 80, 90, 100, 100, 100]
})
# 통계 값 계산
print("평균 점수:", df['score'].mean())
print("최빈값:", df['score'].mode()[0])
print("중앙값:", df['score'].median())
print("표준편차:", df['score'].std())
print("왜도:", df['score'].skew())
print("첨도:", df['score'].kurt())
# 히스토그램 시각화
plt.figure(figsize=(10, 6))
sns.histplot(df['score'], bins=8, kde=True, color='skyblue')
# 평균, 중앙값, 최빈값 시각화
plt.axvline(df['score'].mean(), color='red', linestyle='--', label=f'평균: {df["score"].mean():.2f}')
plt.axvline(df['score'].median(), color='green', linestyle='--', label=f'중앙값: {df["score"].median()}')
plt.axvline(df['score'].mode()[0], color='blue', linestyle='--', label=f'최빈값: {df["score"].mode()[0]}')
plt.title('Score Distribution with Skewness & Kurtosis')
plt.xlabel('Score')
plt.ylabel('Frequency')
plt.legend()
plt.grid(True)
plt.show()
결과:
평균 점수: 81.25
최빈값: 100
중앙값: 85.0
표준편차: 19.594095320493146
왜도: -0.5340954051664979
첨도: -1.2940876149269878
첨도가 -1.29라는 값의 의미는?
- 이 값은 정규분포보다 훨씬 평평한 형태라는 뜻이에요.
- 즉, 점수가 어떤 특정 값에만 몰려 있지 않고 여러 값에 넓게 분산되어 있다는 걸 수치로 말해주는 거예요. 즉 마이너스( - )가 되면 그건 정규분포보다 평평한 분포라는 뜻입니다.
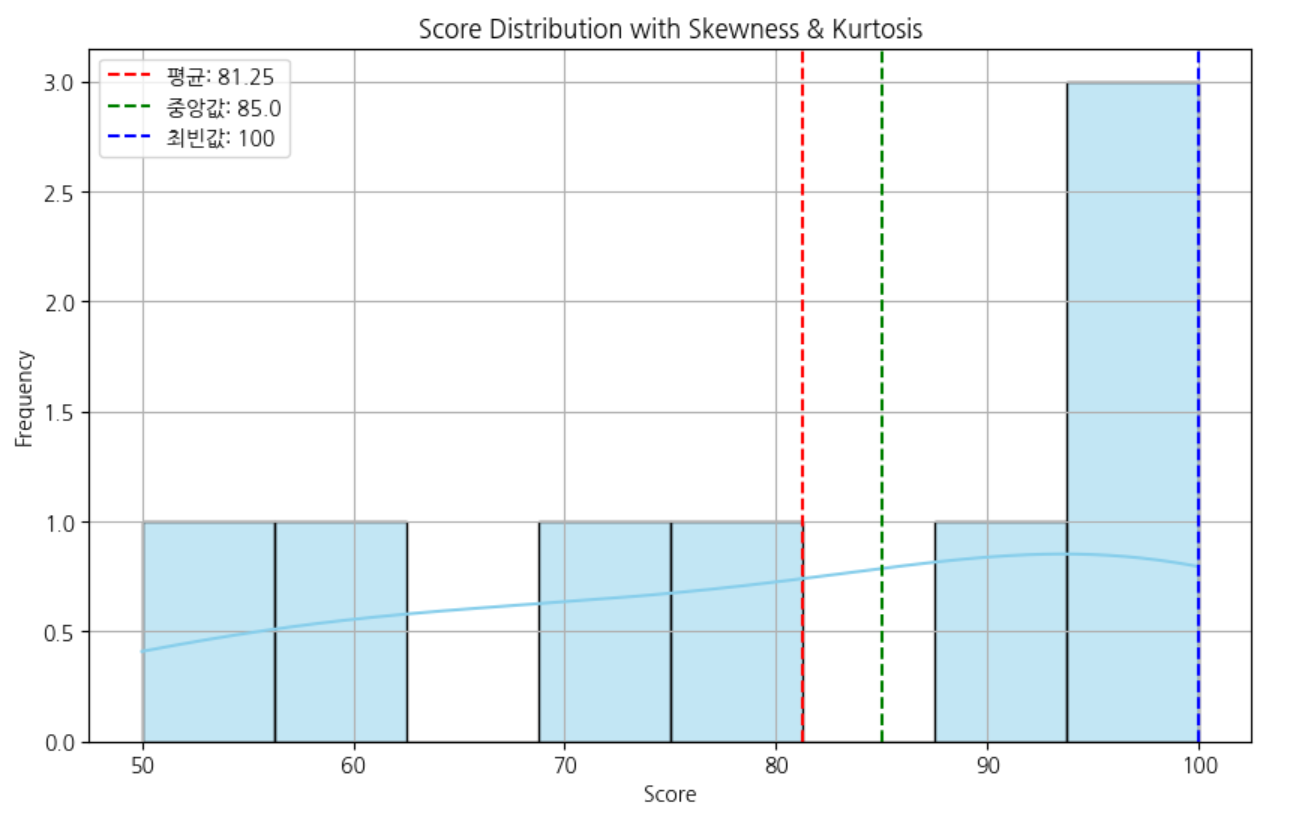 이 그래프는 첨도가 낮은 (평평한) 분포를 보여줍니다.
이 그래프는 첨도가 낮은 (평평한) 분포를 보여줍니다.
- 첨도(Kurtosis)는 데이터의 분포가 중앙에 얼마나 집중되어 있는지를 나타냅니다.
- 그래프를 보면 특정 점수(100점)에 몰려 있는 데이터는 있지만, 나머지 점수들도 50부터 90까지 넓게 퍼져 있습니다.
- 분포의 중심이 뾰족하지 않고 전반적으로 퍼져 있는 평평한 형태입니다.
- 실제로 Pandas로
df['score'].kurt()값을 계산하면 약 -1.29 정도가 나옵니다.
→ 이는 정규분포보다 평평한 분포를 뜻하는 플라티쿠르틱 (platykurtic) 형태입니다.
import pandas as pd
df = pd.read_csv("csv_files/employees_data.csv")
# 평균 (Mean)
print("\n평균 (Mean):")
print(df["salary"].mean()) # 모든 급여의 평균값
# 중앙값 (Median)
print("\n중앙값 (Median):")
print(df["salary"].median()) # 중간에 위치한 값 (50%)
# 최빈값 (Mode)
print("\n최빈값 (Mode):")
print(df["salary"].mode()) # 가장 자주 등장하는 급여
# 분산 (Variance) & 표준편차 (Standard Deviation)
print("\n분산 (Variance):")
print(df["salary"].var()) # 데이터의 퍼짐 정도
print("\n표준편차 (Standard Deviation):")
print(df["salary"].std()) # 분산의 제곱근, 퍼짐 정도를 원 단위로 확인
# 왜도 (Skewness)
print("\n왜도 (Skewness):")
print(df["salary"].skew()) # 분포의 비대칭 정도 (왼쪽/오른쪽 치우침)
# 첨도 (Kurtosis)
print("\n첨도 (Kurtosis):")
print(df["salary"].kurt()) # 분포의 뾰족함 (뾰족 ↔ 평평)
결과:
평균 (Mean):
89866.466
중앙값 (Median):
90171.0
최빈값 (Mode):
0 36445
1 104756
2 112293
3 121519
4 143795
5 144748
Name: salary, dtype: int64
분산 (Variance):
1216300260.6735175
표준편차 (Standard Deviation):
34875.49656526079
왜도 (Skewness):
-0.0005633158265260066
첨도 (Kurtosis):
-1.2256302046834466
시각화
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
# 데이터 로드
df = pd.read_csv("csv_files/employees_data.csv")
# 히스토그램과 KDE 플롯 생성
plt.figure(figsize=(12, 6))
sns.histplot(df["salary"], kde=True)
plt.title("Salary Distribution with KDE")
plt.xlabel("Salary")
plt.ylabel("Frequency")
plt.show()
# 박스 플롯 생성
plt.figure(figsize=(6, 4))
sns.boxplot(y=df["salary"])
plt.title("Box Plot of Salary")
plt.ylabel("Salary")
plt.show()
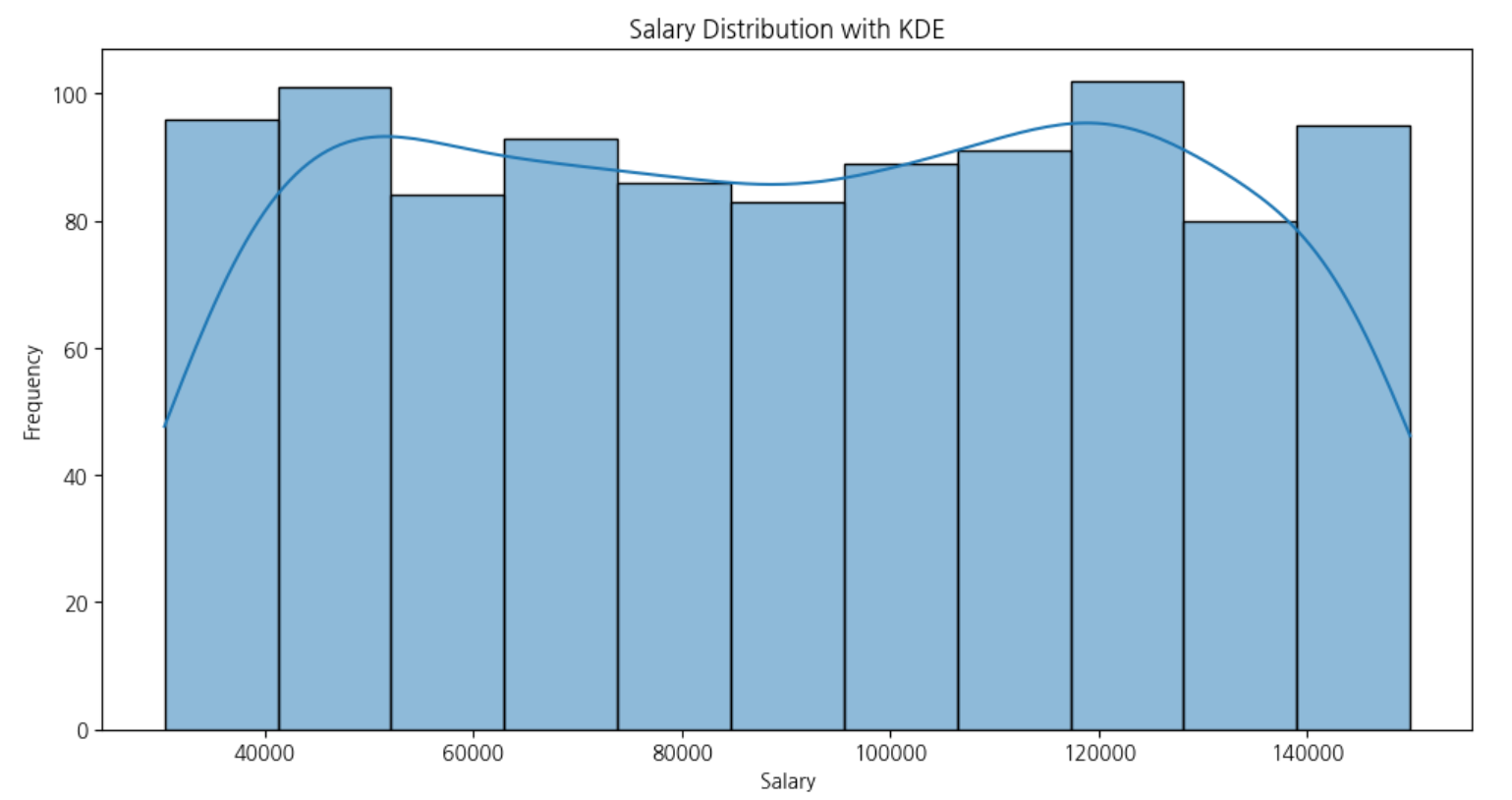
첫 번째 그래프: 히스토그램 + KDE 그래프
 ✔️ 구성
✔️ 구성
- 막대(히스토그램): 급여가 특정 구간에 얼마나 자주 나오는지를 보여줘요.
예:60,000~70,000구간에 있는 직원이 많다면, 그 구간 막대가 높아요. - 곡선(KDE 커널 밀도 추정선): 데이터를 부드럽게 연결한 선이에요. 전체 분포의 형태를 한눈에 파악할 수 있어요.
✔️ 읽는 방법
- 높은 막대 = 그 급여 구간에 속한 사람이 많다.
- KDE 선의 모양 = 분포의 전체적인 흐름
- 한쪽으로 치우치면 왜도(Skewness) 발생
- 뾰족하거나 평평하면 첨도(Kurtosis) 의미
✔️ 활용 예시 이 그래프를 보면 직원들의 급여가 특정 구간에 몰려 있는지, 평균보다 높은 급여자가 많은지 등을 알 수 있어요.
두 번째 그래프: 박스플롯 (Box Plot)
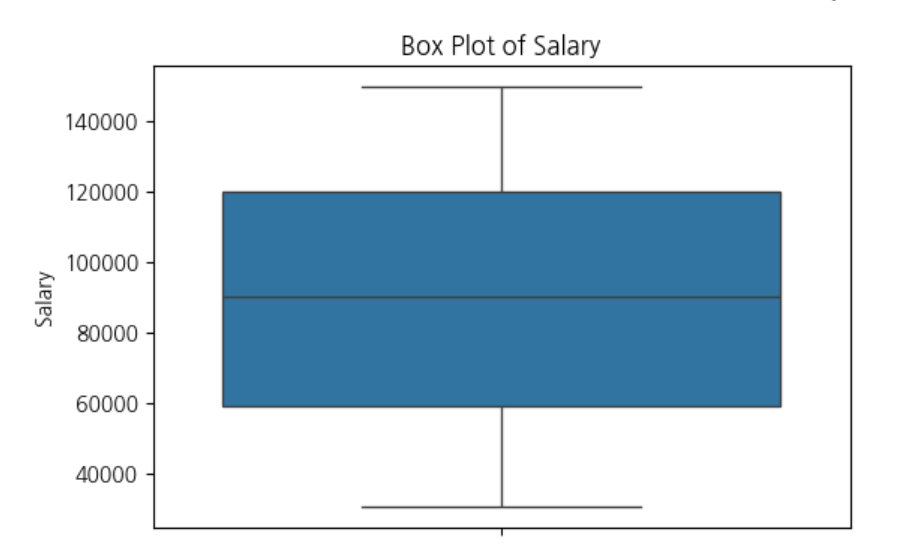 ✔️ 구성
✔️ 구성
- 중앙 가로선: 중앙값 (Median)
- 상자(Box): 중간 50%의 급여 범위 (25%~75% 구간, 즉 IQR)
- 상자 양 끝의 수염(whisker): 대부분의 급여 범위
- 수염 바깥의 점: 이상치 (Outliers) → 극단적으로 높은/낮은 급여자
✔️ 읽는 방법
- 상자의 위치: 급여 분포의 중간이 어디쯤인지 확인 가능
- 중앙선이 한쪽으로 치우쳐 있음: 왜도가 존재함
- 수염이 길거나 점이 많으면: 이상치가 많다
✔️ 활용 예시 이 박스플롯을 보면 급여가 대체로 어느 범위에 몰려 있는지, 이상치가 많은지, 한쪽으로 치우쳤는지 등을 확인할 수 있어요.
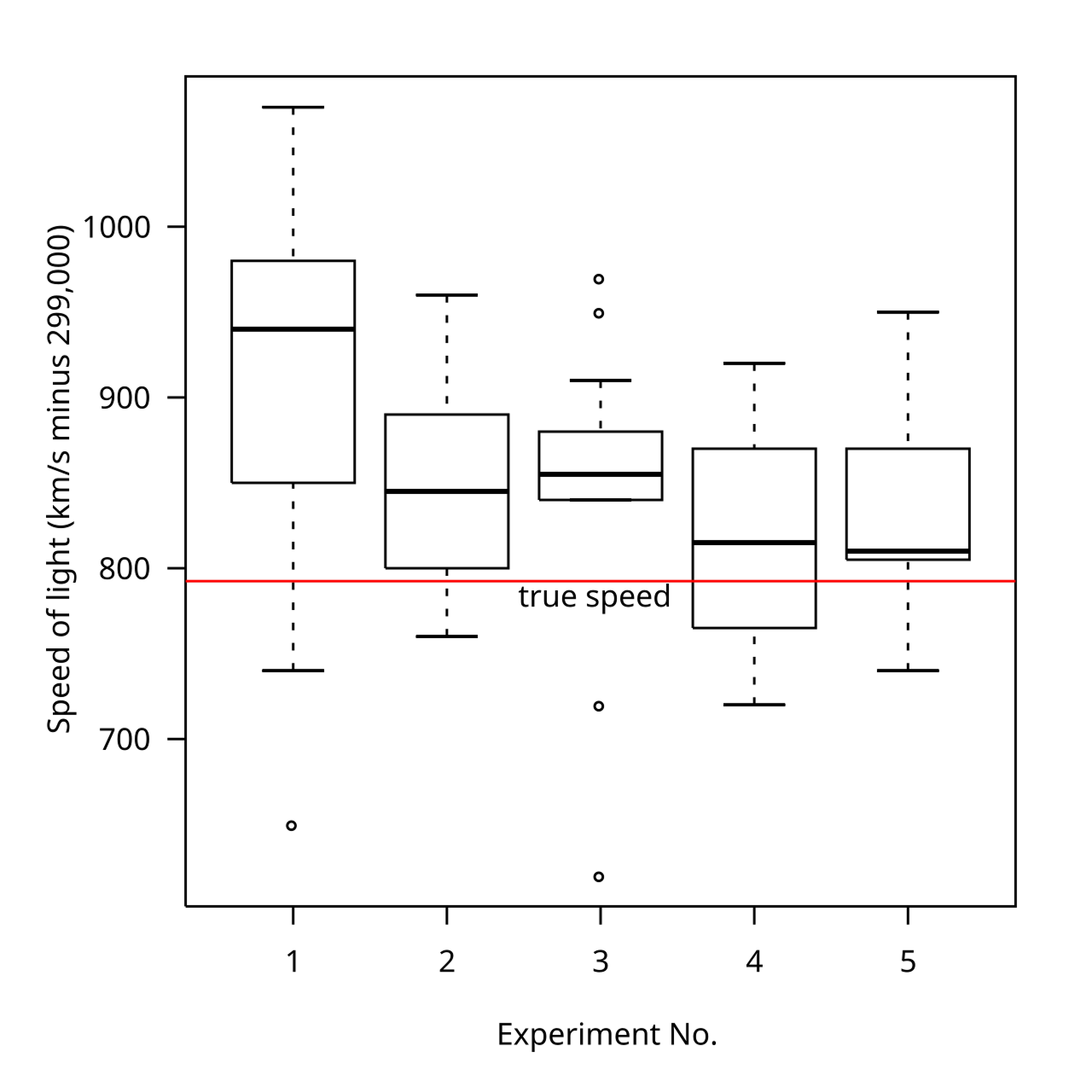
박스플롯을 해석하는 방법:
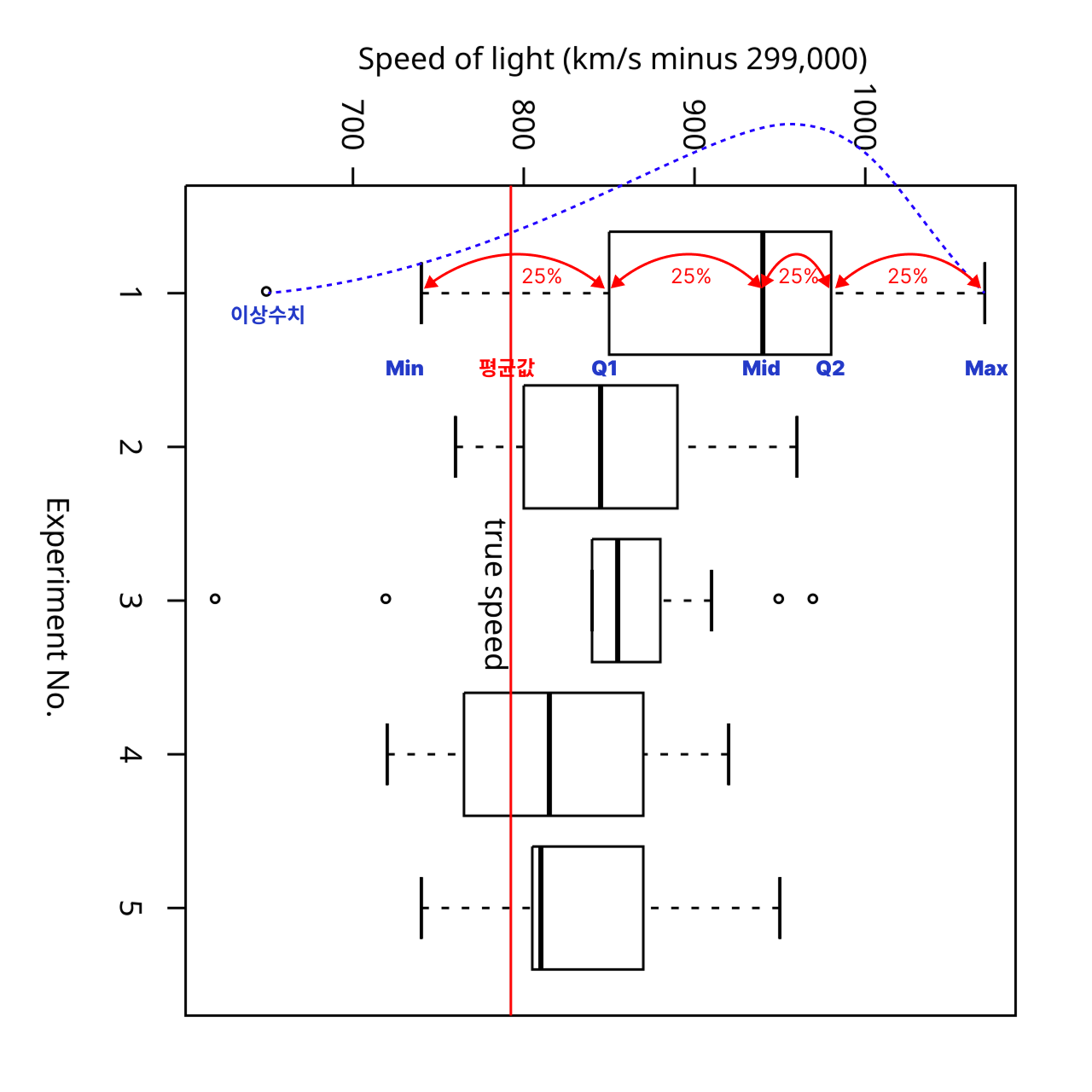
박스플롯 구성 요소 설명
| 용어 | 의미 | 설명 |
|---|---|---|
| Min (최소값) | 이상치를 제외한 최솟값 | 전체 데이터 중 가장 작은 값이 아님! |
| Q1 (제1사분위수) , | 하위 25% 지점 값 | 25% 지점, 박스 왼쪽 끝 |
| Median (중앙값) | 중간에 위치한 값 | 50% 지점, 박스 가운데 굵은 선 |
| Q3 (제3사분위수) | 상위 75% 지점 값 | 75% 지점, 박스 오른쪽 끝 |
| Max (최대값) | 이상치를 제외한 최댓값 | 전체에서 가장 큰 값이 아님! |
| IQR | Q3 - Q1 (사분위 범위) | 데이터가 얼마나 퍼져 있는지 나타냄 |
| 이상치 (Outlier) | 극단적으로 크거나 작은 값 | ○ 또는 * 로 표시됨 |
