함수의 활용 | ✅저자: 이유정(박사)
🔹 재귀 함수(Recursive Function)
재귀 함수는 함수 내부에서 자기 자신을 다시 호출하는 함수입니다.
복잡한 계산을 반복적으로 수행하거나, 수학적으로 정의된 계단식 계산에
적합합니다.
</> 코드로 보는 재귀함수
def countdown(n):
print(n)
countdown(n - 1) # ←이 줄이 핵심! 함수가 자기 자신을 다시 부릅니다.
countdown(5)
countdown()함수 안에서 또 다시countdown()을 호출하고 있어요.- 이렇게 함수가 자기 자신을 부르면 '재귀 함수'라고 부릅니다.
n값을 하나씩 줄이면서, 숫자를 출력하다가 계속 호출되기 때문에 멈추지 않아요!- 그래서 반드시 멈추는 조건(종료 조건)이 필요해요!
⚠️ 주의: 위의 코드를 실행하면 기본 종료 조건(base case)이 없어서 무한히 자기 자신을 호출합니다:
실행결과:
5
4
3
2
1
0
-1
-2
...
RecursionError: maximum recursion depth exceeded
- 파이썬은 재귀 호출을 일정 횟수 이상 허용하지 않도록 제한하고 있는데, 기본 한도는 약 1,000번입니다.
| 항목 | 설명 |
|---|---|
| 자기 호출 | 함수가 자기 자신을 내부에서 다시 부름 |
| 종료 조건(Base Case) | 반드시 있어야 함! 없으면 무한 반복으로 오류 발생 |
| 반복 대체 | 반복문 없이도 반복적인 로직 구현 가능 |
📖 재귀 함수 구조 예시:
def recursive_function():
if 종료조건:
return 결과값
else:
return recursive_function()
◽ 팩토리얼(Factorial)을 재귀로 구현하기 (수학정의)

팩토리얼은 자연수 n에 대해 1부터 n까지의 모든 정수를 곱한 값입니다.
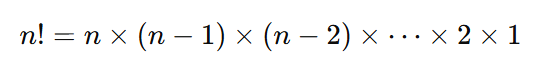
n! = n × (n-1) × (n-2) × ... × 1- 예:
5! = 5 × 4 × 3 × 2 × 1 = 120
💬 보충설명: 곱셈은 교환법칙이 있기 때문에 어떤 순서로 곱해도 결과는 같습니다. 5! 이렇게 사용하는 이유는 가독성 때문입니다.
📝 문제1] N개의 서로 다른 숫자가 주어질 때, 이 중에서 K개를 순서 없이 뽑는 경우의 수를 구하시오. [경우의 수 계산]
</> 입력:
N = 5 # 5명의 친구들
K = 3 # 3명씩 조합
해석: 친구 5명(A, B, C, D, E) 중에서 3명을 뽑고 싶어요.
이때 순서를 생각하지 않고, 어떤 조합이 가능한지 알고 싶어요.
📖 말의 의미:
-
순열(Permutation)이란? 순서를 중요하게 생각하는 것으로 ABCD등 순서가 있는것을 말합니다.
-
조합 (Combination)이란? 순서는 상관없고 A, B, C 중 2명을 뽑으면 AB나 BA는 같은 조합을 말합니다.
여기에서 가능한 조합은 모두 10개입니다.
A, B, C
A, B, D
A, B, E
A, C, D
A, C, E
A, D, E
B, C, D
B, C, E
B, D, E
C, D, E
📖 조합의 공식은 다음과 같습니다. <p align="left"> <img src="Pasted image 20250519180853.png" width="285"> <img src="Pasted image 20250519181110.png" width="220"> </p> 여기서
n!= 전체 사람 수에서 모든 경우의 순열 수k!= 고른 사람의 내부 순서(중복)를 제거(n - k)!= 남은 사람의 경우의 수 제거
계산을 해보면:
- 5! = 5 × 4 × 3 × 2 × 1 = 120
- 3! = 3 × 2 × 1 = 6
- 2! = 2 × 1 = 2
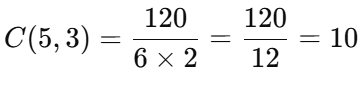
🖨️ 출력 결과:
10
✅ 정답 코드:
import math # 수학 함수들이 들어있는 파이썬 모듈
def combination(n, k):
# 조합 공식에 따라 계산: n! / (k! * (n - k)!)
return math.factorial(n) // (math.factorial(k) * math.factorial(n - k))
# 정수로 만들기 위해 //로 정수 나눗셈은 한다.
print(combination(5, 3)) # 5명 중 3명 뽑기 → 출력: 10
문제풀이: 친구 5명이 있어요: A, B, C, D, E 이 중 3명을 팀으로 뽑는 방법이 궁금한 거예요 순서를 따지지 않고 조합을 구하는 거예요
🔹 수학 정의 그대로 적용한 재귀함수
수학에서 팩토리얼 정의
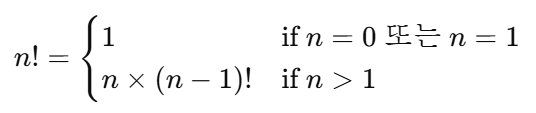 📖 풀어서 쓰면 이렇게 됩니다:
어떤 수
📖 풀어서 쓰면 이렇게 됩니다:
어떤 수 n의 팩토리얼을 구하고 싶다면,
-
만약
n이 0이거나 1이면, 결과는 무조건 1이다. -
만약
n이 2 이상이면,
→n에다가n-1의 팩토리얼을 곱해서 계산한다. -
여기서
1! = 1이기 때문에 재귀가 멈추는 조건이 되는 거예요.
5! = 5 × 4!
= 5 × 4 × 3!
= 5 × 4 × 3 × 2!
= 5 × 4 × 3 × 2 × 1!
= 5 × 4 × 3 × 2 × 1 = 120
위의 수학적 내용을 코드로 옮기면 다음과 같습니다:
</> 예시 코드:
def factorial_math(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial_math(n - 1) # n! = n * (n-1)!
</> 호출:
print("5! =", factorial_math(5))
🖨️ 출력 결과:
5! = 120
🔍 해설:
factorial_recursive(5)를 호출하면, 내부에서 다음과 같이 계산됩니다:
factorial_recursive(5)
→ 5 * factorial_recursive(4)
→ 5 * 4 * factorial_recursive(3)
→ 5 * 4 * 3 * factorial_recursive(2)
→ 5 * 4 * 3 * 2 * factorial_recursive(1)
→ 5 * 4 * 3 * 2 * 1 = 120
n == 1이 되면 더 이상 함수가 호출되지 않고 종료됨 (종료 조건)
🔹 반복문과 재귀 함수의 비교
| 항목 | 반복문 (for, while) |
재귀 함수 (재귀 호출) |
|---|---|---|
| 정의 | 일정한 횟수 또는 조건에 따라 코드를 반복 실행 | 함수가 자기 자신을 호출하여 반복 수행 |
| 종료 방식 | 조건식이 False가 되면 종료 |
종료 조건(Base Case)에 도달하면 종료. |
| 장점 | 실행 속도가 빠르고 메모리 효율적 | 수학적 표현과 동일한 구조로 가독성 높음 |
| 단점 | 복잡한 알고리즘 표현이 어려울 수 있음 | 호출이 깊어지면 RecursionError 발생 가능 |
| 💬 종료 조건(Base Case): |
더 이상 자기 자신을 호출하지 않아도 되는 조건이 되었을 때,
재귀 호출을 멈추고 함수 실행을 끝
</> 예시 코드: 반복문으로 구현한 팩토리얼
# 반복문 버전
def factorial_for(n):
result = 1
for i in range(1, n + 1):
result *= i
return result
print("반복문 방식:", factorial_for(5))
# 재귀함수 버전
def factorial_rec(n):
if n == 0 or n == 1:
return 1
else:
return n * factorial_rec(n - 1)
print("재귀 함수 방식:", factorial_rec(5)) # 출력: 120
🖨️ 출력 결과:
반복문 방식: 120
재귀 함수 방식: 120
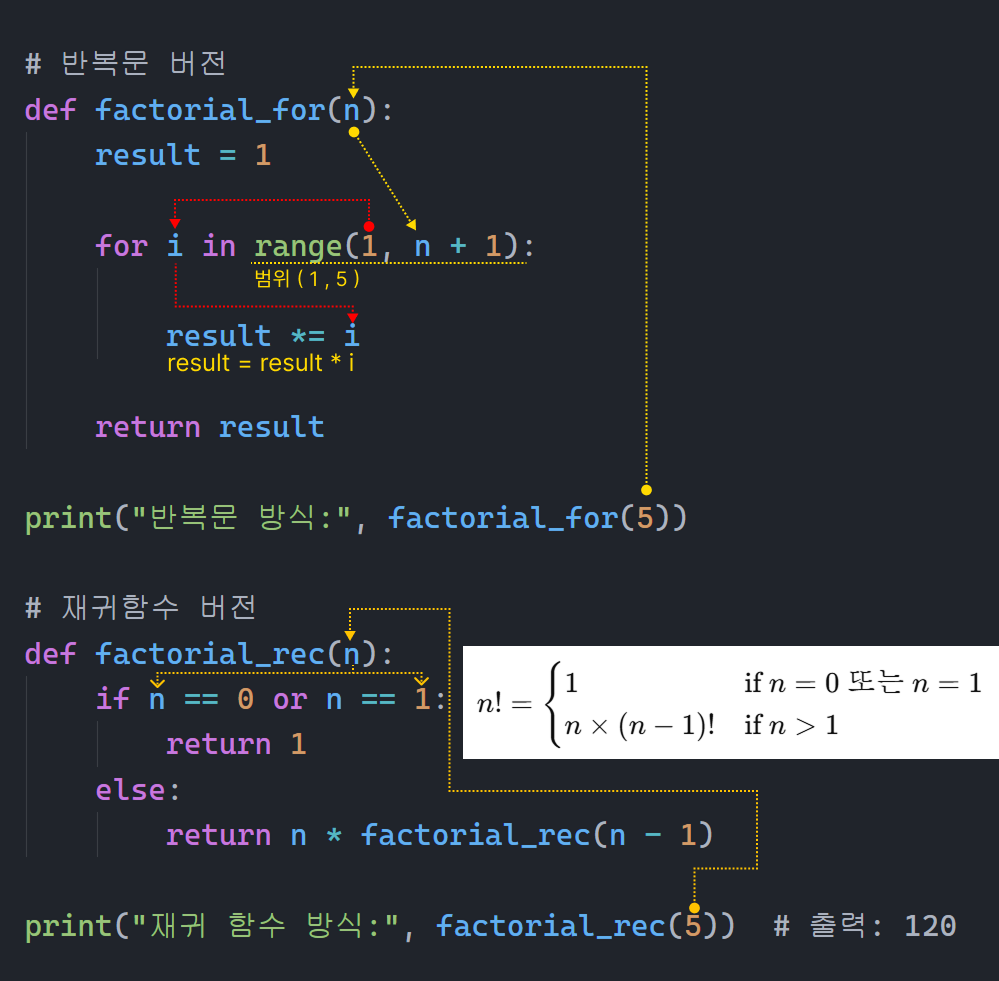
🔍 설명:
n == 1일 때 종료- 그 외에는
n * factorial_rec(n - 1)형태로 계속 자기 자신을 호출 - 함수 호출이 스택에 쌓이기 때문에 메모리 사용량이 많음
- 하지만 수학적 구조를 그대로 코드에 옮겨 놓은 것처럼 우아하고 간결함
📝 문제1] countdown() 함수를 만들어 숫자 n부터 1까지 1씩 감소하며 출력하세요. 단, 재귀 함수를 사용해야 하며, 마지막에는 "발사!"라는 문장을 출력해야 합니다.
countdown(5)
🖨️ 출력 결과:
5
4
3
2
1
발사!
✅ 정답 코드:
def countdown(n):
if n == 0: # Base Case 종료조건
print("발사!") # n이 0이 되면 출력
return
print(n)
countdown(n - 1)
countdown(5)
🔍 해설:
countdown(n)은 숫자n을 출력한 뒤,
다시countdown(n-1)을 호출해서 숫자를 하나 줄입니다.- 이 작업은
n이 0이 될 때까지 반복됩니다.
📝 문제2] 문자열을 거꾸로 출력하는 재귀 함수를 만들어보세요.
reverse_print(text) 함수는 문자열을 인자로 받아,
문자열의 마지막 문자부터 첫 문자까지 한 글자씩 재귀적으로 출력해야 합니다.
reverse_print("hello")
🖨️ 출력 결과:
o
l
l
e
h
✅ 정답 코드:
def reverse_print(text):
if text == "":
return # 종료 조건: 더 이상 출력할 문자가 없으면 종료
print(text[-1]) # 마지막 문자 출력
reverse_print(text[:-1]) # 마지막 문자를 제외한 나머지를 재귀 호출
reverse_print("hello")
🔍 해설:
text == ""이면 빈 문자열이므로 함수 종료 (Base Case)print(text[-1]): 문자열의 마지막 글자를 출력reverse_print(text[:-1]): 마지막 문자를 제외한 나머지 문자열로 재귀 호출
</> 실행 흐름: "abc" :
reverse_print("abc")
→ print("c")
→ reverse_print("ab")
→ print("b")
→ reverse_print("a")
→ print("a")
→ reverse_print("")
→ 종료
🔹 피보나치 수열(Fibonacci Sequence)
피보나치 수열은 앞의 두 수를 더해서 다음 수를 만들어 나가는
수열입니다.
수학적 정의
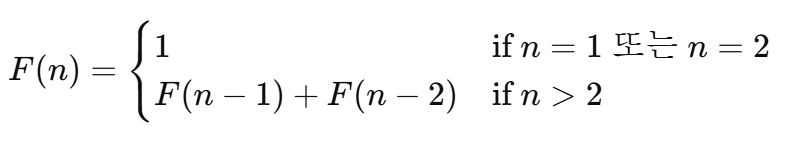
📘 정의:
f(1) = 1
f(2) = 1
f(n) = f(n-1) + f(n-2)
🔢 예시:
f(1) = 1
f(2) = 1
f(3) = f(2) + f(1) = 1 + 1 = 2
f(4) = f(3) + f(2) = 2 + 1 = 3
f(5) = f(4) + f(3) = 3 + 2 = 5
f(6) = f(5) + f(4) = 5 + 3 = 8
f(7) = f(6) + f(5) = 8 + 5 = 13
피보나치수열은 관찰된 자연의 규칙을 수학적으로 나타낸 공식입니다. 토끼의 탄생을 수열로 만든 공식입니다.
f(5) = f(4) + f(3) 이게 무슨 뜻이냐면??
| 달 | 설명 |
|---|---|
| 1월 | 1쌍 (시작) |
| 2월 | 1쌍 (아직 번식 안 됨) |
| 3월 | 2쌍 (1월 쌍이 새끼 낳음) |
| 4월 | 3쌍 (1월쌍이 또 낳고, 2월쌍은 아직 못 낳음) |
| 5월 | 5쌍 (2월쌍이 첫 출산, 3월쌍은 아직) |
| 6월 | 8쌍 (3쌍 + 5쌍 → 앞 두 달 수를 더함) |
→ 즉, 현재 달의 토끼 수는 지난 두 달의 토끼 수를 더한 것!
즉,
f(3)은 3개월차 토끼쌍으로 2쌍을 낳고
f(4)는 4개월차 토끼쌍은 3쌍을 낳는다는 의미입니다.
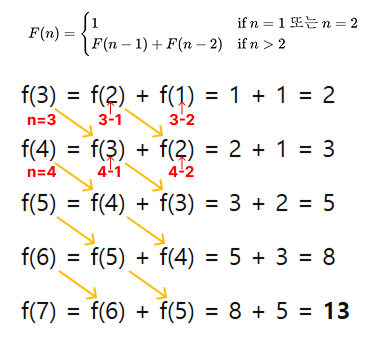
- 위의 이미지를 보고 피보나치 수열을 이해하세요.
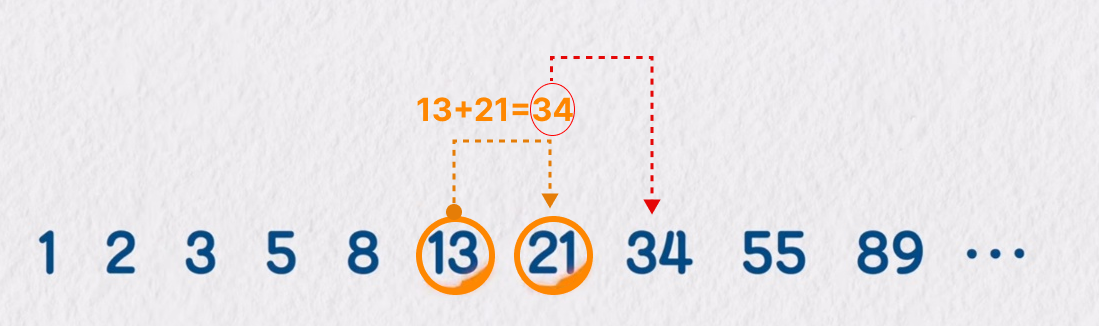
- 두개를 더한 값이 다음수가 되는 방식이 피보나치 수열입니다.
✅ 피보나치 수열의 응용 분야
| 분야 | 활용 예시 |
|---|---|
| 자연 현상 (생물학) | - 해바라기 씨앗의 배열 <br>- 소라 껍질의 나선 <br>- 소나무 잎·꽃잎 개수 <br>- DNA의 회전 구조 |
| 미술 · 디자인 | - 황금비(Golden Ratio)와 연결되어 균형감 있는 디자인 <br>- 로고 디자인, UI/UX, 건축물 비례 |
| 건축 · 구조물 | - 파르테논 신전, 피라미드 등 고대 건축물에 황금비 적용 <br>- 인간이 아름답다고 느끼는 비율을 피보나치로 계산 |
| 컴퓨터 과학 | - 재귀 함수 학습 예제 <br>- 알고리즘 최적화 (동적 계획법, 메모이제이션) <br>- 점화식 구조 이해 |
| 금융 · 투자 분석 | - 피보나치 되돌림(Fibonacci Retracement): 주식, 코인 등에서 가격 조정 구간 예측 도구로 사용 |
| 음악 | - 작곡 시 박자/음의 배열에서 피보나치 수 사용 <br>- 리듬 구조나 음표 길이 등에서 자연스러운 흐름 생성 |
| 뇌과학 · 신경망 모델링 | - 피보나치 수 구조를 활용한 뉴런 신호 전달 모델 |
| AI · 알고리즘 설계 | - 자연 기반 패턴 인식, AI의 규칙 기반 시퀀스 예측 문제에 활용됨 |
</> 예시코드: 재귀 함수로 피보나치 수열 구현
def fibonacci(n):
if n == 1 or n == 2: # 종료 조건
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
# return은 조건이 맞지 않는 False일때만 실행됨
for i in range(1, 8): # 1부터 7까지 출력
print(f"f({i}) =", fibonacci(i)) # i는 n에 전달되는 인자
# 정훈님코드
def fibonacci(n):
if n == 1 or n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
print(fibonacci(6))
- 이 함수에서
return fibonacci(n - 1) + fibonacci(n - 2)는if조건이False일 때만 실행돼요.
n 변수를 대입해보면 다음과 같습니다.
fibonacci(i) → i = 1 → n = 1
if n == 1 or n == 2 → True → return 1
fibonacci(1) : n == 1 → 종료 조건 → return 1
fibonacci(2) : n == 2 → 종료 조건 → return 1
fibonacci(3) :
fibonacci(2) + fibonacci(1) → 1 + 1 = 2
fibonacci(4) :
fibonacci(3) + fibonacci(2)
= (fibonacci(2) + fibonacci(1)) + fibonacci(2) = (1 + 1) + 1 = 3
fibonacci(5) :
fibonacci(4) + fibonacci(3)
= (fibonacci(3) + fibonacci(2)) + (fibonacci(2) + fibonacci(1))
= ((1 + 1) + 1) + (1 + 1)
= (2 + 1) + 2 = 3 + 2 = 5
fibonacci(6) :
fibonacci(5) + fibonacci(4)
= (fibonacci(4) + fibonacci(3)) + (fibonacci(3) + fibonacci(2))
= ((fibonacci(3) + fibonacci(2)) + (fibonacci(2) + fibonacci(1)))
+ ((fibonacci(2) + fibonacci(1)) + fibonacci(2))
= ((1+1)+1 + 1+1) + (1+1 + 1)
= (2+1+2) + (2+1) = 5 + 3 = 8
🖨️ 출력 결과:
f(1) = 1
f(2) = 1
f(3) = 2
f(4) = 3
f(5) = 5
f(6) = 8
f(7) = 13
🔍 해설:
if n == 1 or n == 2:피보나치 수열의 처음 두 항은 항상 1이므로, 이때는 더 계산하지 않고 1을 바로 돌려줍니다 (종료 조건)return fibonacci(n - 1) + fibonacci(n - 2): 그렇지 않다면, 앞의 두 항을 다시 함수로 계산해서 더해줍니다 (재귀 호출)for i in range(1, 8):f(1)부터f(7)까지의 결과를 차례대로 출력합니다
📝 문제1] n번째 피보나치 수 계산하기
정수를 하나 입력받아 n번째 피보나치 수를 구하세요.
단, 재귀 함수를 사용해야 합니다.
print(fibonacci(5)) # 5번째 피보나치 수를 출력
🖨️ 출력 결과:
5
✅ 정답:
def fibonacci(n):
if n == 1 or n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2) # 재귀함수
print(fibonacci(5))
🔍 해설:
- 피보나치 수열은
f(n) = f(n-1) + f(n-2)의 규칙을 따릅니다. n == 1 or 2일 때는 값이 항상 1이므로 종료 조건으로 사용합니다.
✅ 실제 계산 흐름:
fibonacci(5)
= fibonacci(4) + fibonacci(3)
= (fibonacci(3) + fibonacci(2)) + (fibonacci(2) + fibonacci(1))
= ((fibonacci(2) + fibonacci(1)) + 1) + (1 + 1)
= ((1 + 1) + 1) + (1 + 1)
= 5
📝 문제2] 1부터 n까지 피보나치 수열 출력하기 정수 n이 주어졌을 때, f(1)부터 f(n)까지 피보나치 수열을 한 줄씩 출력하는 프로그램을 작성하세요. 단, 재귀 함수를 사용해서 구현하세요.
print_fibonacci(6)
🖨️ 출력 결과:
1
1
2
3
5
8
✅ 정답:
# 재귀함수 방식
def fibonacci(n):
if n == 1 or n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
def print_fibonacci(n):
for i in range(1, n + 1):
print(fibonacci(i))
print_fibonacci(6)
# for문 방식
def fibonacci_sum(n):
a, b = 1, 1
for i in range(1, n + 1):
if i == 1 or i == 2:
print(1)
else:
a, b = b, a + b
print(b)
print(fibonacci_sum(6))
🔍 해설:
fibonacci(n)은 재귀 함수로 정의되어 있으며,print_fibonacci(n)함수는 1부터 n까지 반복문으로 출력합니다.- 재귀 함수 내부는 반복문을 쓰지 않지만, 전체 수열 출력을 위해 외부에
for문을 함께 사용합니다.
%201%201.png)

📝 문제3] 피보나치 수열의 합 구하기
정수 n이 주어졌을 때, f(1) + f(2) + ... + f(n)
즉, n번째 피보나치 수까지의 누적 합을 구하는 프로그램을 작성하세요.
반드시 재귀 함수만을 사용하여 구현해야 합니다. (※ 반복문 없이, 재귀만 사용)
print(fibonacci_sum(5))
🖨️ 출력 결과:
12
✅ 정답:
def fibonacci(n):
if n == 1 or n == 2:
return 1
return fibonacci(n - 1) + fibonacci(n - 2)
def fibonacci_sum(n):
if n == 1:
return 1
return fibonacci(n) + fibonacci_sum(n - 1)
print(fibonacci_sum(5))
🔍 해설:
- 이 문제는 두 개의 재귀 함수가 필요합니다:
fibonacci(n)→ n번째 피보나치 수를 재귀로 계산fibonacci_sum(n)→ 이전까지의 합을 재귀로 누적
- 종료 조건으로
n == 1일 때는1을 반환하여 누적이 멈춥니다. - 결과적으로
f(1) + f(2) + ... + f(n)이 계산됩니다. - 반복문 없이 완전히 재귀만으로 합계를 구하는 고급 문제입니다.
🔹 재귀 함수의 문제: UnboundLocalError
UnboundLocalError란?
함수 내부에서 어떤 변수를 사용하려고 했는데,
그 변수가 아직 값이 정해지지 않았을 때 발생하는 오류입니다.
</> 예시코드: 쉽게 말하면
count = 0 # 전역 변수 선언
def counter():
count += 1 # ❗ 아직 count가 뭔지 모름
return count
print(counter())
- 여기서
count += 1은count = count + 1과 같은 뜻이에요. - 그런데 왼쪽은 대입, 오른쪽은 읽기입니다.
count라는 값을 먼저 읽으려고 했는데,
함수 안에는 아직count에 대한 값이 없어요 → 에러 발생!
🛑 출력 결과:
UnboundLocalError: local variable 'count' referenced before assignment
🤔 왜 이런 일이 생겼을까?
- 파이썬은 함수 안에서 변수에 값을 할당하면,
그 변수는 지역 변수(local variable)라고 자동으로 간주합니다 - 그래서
count는 전역에 있더라도, 함수 안에서는 새로운 count라고 생각합니다. - 그런데 그 새 count는 아직 값이 없는데 사용하려고 하니까 오류가 나는 것입니다.
</> 수정된 코드: 전역 변수로 명확히 알려주기
count = 0 # 전역 변수 선언
def counter():
global count # 전역 변수를 사용하겠다고 명시
count += 1
return count
print(counter()) # 1
print(counter()) # 2
- 파이썬에서는 함수 안에서 전역 변수(global variable)를 사용하려면
global이라는 키워드를 사용해서 "전역 변수야!"라고 명시해줘야 합니다.
🖨️ 출력 결과:
1
2
◽ nonlocal 키워드란?
nonlocal은 중첩 함수(함수 안에 함수)가 있을 때,
바깥쪽 함수의 지역 변수를 안쪽 함수에서 수정하고 싶을 때 사용하는 키워드입니다.
❌ nonlocal 없이 바깥 변수를 수정할 수 있을까?
def outer():
count = 0
def inner():
count += 1 # ❌ 오류 발생: 지역 변수로 간주됨
print("inner:", count)
inner()
print("outer:", count)
outer()
🛑 출력 결과:
UnboundLocalError: local variable 'count' referenced before assignment
</> 올바른 코드: nonlocal 사용 예시
def outer():
count = 0 # 바깥 함수의 지역 변수
def inner():
nonlocal count # 바깥 count를 수정할 거야!
count += 1
print("inner:", count)
inner()
print("outer:", count)
outer()
🖨️ 출력 결과:
inner: 1
outer: 1
🔍 해설
count는outer()함수의 지역 변수입니다.inner()는 그 안에 있는 중첩 함수예요.nonlocal count를 쓰면,inner()함수 안에서도outer()함수의count를 읽고 수정할 수 있게 됩니다.global은 전역 범위를 대상으로 하고,nonlocal은 바로 한 단계 바깥 함수의 지역 변수만 대상으로 해요.
📝 문제1] 지역 변수 사용 오류 (UnboundLocalError) 아래 함수는 숫자를 1씩 증가시키려는 코드입니다. 하지만 실행하면 오류가 발생합니다. 오류의 원인을 파악하고 코드를 수정하세요.
def counter():
count += 1
return count
print(counter())
🖨️ 출력 결과 (오류 힌트):
UnboundLocalError: local variable 'count' referenced before assignment
✅ 정답:
count = 0 # 전역 변수 정의
def counter():
global count # 전역 변수를 쓰겠다고 명시
count += 1
return count
print(counter()) # 1
🔍 해설:
- 함수 내부에서
count += 1을 실행하면, 파이썬은count를 지역 변수로 간주합니다. - 그런데 그 변수는 아직 초기화되지 않았기 때문에 사용 전에 오류가 발생합니다.
- 전역 변수
count를 사용하려면global키워드로 전역 범위의 변수임을 명시해야 합니다.
문제2] 중첩 함수에서 바깥 변수 접근 오류
다음 코드는 함수 안에 있는 inner() 함수가 바깥쪽 함수 outer()의 변수 x를 사용해서 값을 1 증가시키려고 합니다. 하지만 실행하면 오류가 발생합니다. 오류를 수정해보세요.
def outer():
x = 0
def inner():
x += 1
print("inner:", x)
inner()
print("outer:", x)
outer()
🖨️ 출력 결과 (오류 힌트):
UnboundLocalError: local variable 'x' referenced before assignment
✅ 정답:
def outer():
x = 0
def inner():
nonlocal x # 바깥 함수의 지역 변수 사용
x += 1
print("inner:", x)
inner()
print("outer:", x)
outer()
🔍 해설:
inner()함수는outer()함수 안에 정의된 중첩 함수입니다.x는outer()함수의 지역 변수이지만,
inner()에서 값을 할당하려고 하면 자체적으로 새로운 지역 변수로 간주되어 오류가 납니다.- 이럴 때는
nonlocal x를 사용하면
→ 바깥 함수(outer)의 지역 변수x를 가져와서 수정할 수 있습니다.
📝 문제3] 지역 변수와 global 혼용 문제
전역 변수 total을 사용하여 누적합을 계산하려는 코드입니다.
그런데 함수 내부에서 잘못된 위치에 변수를 선언하여 오류가 발생합니다.
문제를 분석하고 고치세요.
total = 0
def add(n):
print("기존 합:", total)
total += n
return total
print(add(10))
🖨️ 출력 결과 (오류 힌트):
UnboundLocalError: local variable 'total' referenced before assignment
✅ 정답:
total = 0
def add(n):
global total # 전역 변수 사용 선언
print("기존 합:", total)
total += n
return total
print(add(10)) # 10
🔍 해설:
total은 전역 변수지만, 함수 안에서+=연산을 수행하면 파이썬은 이를 새로운 지역 변수로 처리하려고 합니다.- 그래서
print(total)에서 아직 정의되지 않은 지역 변수를 읽으려 해서 오류가 발생합니다. global total을 사용하여 전역 변수 total을 참조하겠다고 명시해야 오류가 해결됩니다.
🔹 메모화 (Memoization)
메모화(Memoization)는 함수의 결과값을 저장(cache) 해두고, 같은 입력
이 들어왔을 때 다시 계산하지 않고 저장된 값을 재사용하는 최적화 기법입
니다.
🤔 언제 사용하나요?
- 재귀 함수에서 같은 계산을 반복할 때
- 계산 비용이 매우 큰 함수일 때
- 특히 피보나치 수열, 경로 탐색, DP(동적 프로그래밍) 문제에 유용
❌ </> 비효율적인 재귀 피보나치 함수: 메모화 없이 재귀 호출 시의 문제
def fib(n):
if n <= 2:
return 1
return fib(n-1) + fib(n-2)
print(fib(35)) # 매우 느림
🛑 문제점:
- 같은 값(
fib(30),fib(29)등)을 수백 번 중복 계산 - 시간 복잡도:
O(2^n)(지수 시간) fib(35)만 해도 수천~수만 번 함수 호출됨
◽ 메모화(Memoization) 적용한 개선 방법
📖 메모화의 핵심 문법(Syntax)
# 1. 저장용 딕셔너리 선언
memo = {}
# 2. 함수 정의 안에서:
if n in memo: # 이미 계산된 값인지 확인
return memo[n] # 저장된 결과 재사용
# 3. 새로 계산한 결과 저장
memo[n] = result
</> 딕셔너리를 이용한 메모화 구현:
memo = {} # 메모(저장소)
def fib(n):
if n in memo: # 이미 계산된 값이면
return memo[n] # 바로 반환
if n <= 2:
result = 1
else:
result = fib(n-1) + fib(n-2)
memo[n] = result # 계산 결과 저장
return result
print(fib(35)) # 매우 빠름
💬 보충설명:
-
개념: 중복 계산을 피하기 위해 결과를 저장하고 재사용하는 기법입니다.
-
도구: 딕셔너리 사용 (
memo = {})하며 계산한 값들은키:값형태로 저장됩니다. -
적용대상: 재귀 함수, 동적 프로그래밍(Dynamic Programming), 중복 호출이 많은 계산 문제
-
기대효과: 동일한 함수 호출을 피해서 속도 향상, 수천 배 성능 향상도 가능함
📝 문제1] n번째 피보나치 수 계산 (메모화 적용)
정수 n이 주어졌을 때, n번째 피보나치 수를 출력하는 함수를 작성하세요.
반드시 재귀 함수 + 메모화(memoization)를 적용하세요.
print(fib(6))
🖨️ 출력 결과:
8
✅ 정답 코드:
memo = {}
def fib(n):
if n in memo:
return memo[n]
if n <= 2:
result = 1
else:
result = fib(n - 1) + fib(n - 2)
memo[n] = result
return result
print(fib(6))
🔍 해설:
fib(n)은 기본적으로f(n-1) + f(n-2)구조의 재귀 함수입니다.- 메모화(
memo)를 통해 이미 계산한 값을 저장해두고
같은 계산을 다시 하지 않게 하므로 성능이 향상됩니다. fib(6)은1 1 2 3 5 8중 6번째 →8입니다.
📝 문제2] 1부터 n까지 피보나치 수를 모두 출력 (메모화 포함)
정수 n이 주어졌을 때, f(1)부터 f(n)까지 피보나치 수열을 한 줄에 출력하세요. 재귀 함수 + 메모화를 적용하여 구현하세요.
print_fibonacci(7)
🖨️ 출력 결과:
1 1 2 3 5 8 13
✅ 정답 코드:
memo = {}
def fib(n):
if n in memo:
return memo[n]
if n <= 2:
result = 1
else:
result = fib(n - 1) + fib(n - 2)
memo[n] = result
return result
def print_fibonacci(n):
for i in range(1, n + 1):
print(fib(i), end=" ")
print_fibonacci(7)
🔍 해설:
fib(n)은 메모화를 적용한 재귀 함수로, 이전 계산값을 저장함print_fibonacci(n)은1부터n까지 반복하면서 각각의fib(i)를 출력함- 메모화를 통해 중복 계산 없이 빠르게 결과를 출력할 수 있음
📝 문제3] n번째 피보나치 수까지의 총합 구하기 (재귀 + 메모화)
정수 n이 주어졌을 때, f(1) + f(2) + ... + f(n)
즉, n번째 피보나치 수까지의 누적 합을 구하는 프로그램을 작성하세요.
반드시 재귀 + 메모화를 사용해야 합니다.
print(fibonacci_sum(6))
🖨️ 출력 결과:
20
- 계산 설명:
1 + 1 + 2 + 3 + 5 + 8 = 20
✅ 정답 코드:
memo = {}
def fib(n):
if n in memo:
return memo[n]
if n <= 2:
result = 1
else:
result = fib(n - 1) + fib(n - 2)
memo[n] = result
return result
def fibonacci_sum(n):
if n == 1:
return fib(1)
return fib(n) + fibonacci_sum(n - 1)
print(fibonacci_sum(6))
🔍 해설:
fib(n)은 메모화를 적용한 피보나치 계산 함수fibonacci_sum(n)은 재귀를 이용해 누적합을 구함fib(n)을 계속 재사용하지만,memo덕분에 이미 계산된 값은 다시 계산하지 않음- 시간복잡도는
O(n)으로 최적화됨
📝 문제4] 피보나치 수열을 계산할 때 중복 호출을 피하려면 어떻게 해야 하나요?
A. print() 사용 B. 변수를 global로 만든다 C. 메모화 기법을 사용한다 (정답) D. while문으로 바꾼다
✅ 정답: C. 메모화 기법을 사용한다
🔹 조기 리턴(Early Return)
조기 리턴이란, 함수 실행 도중 조건을 만족하면 더 이상 진행하지 않고
즉시 종료(return) 하는 기법입니다.
🤔왜 필요한가요?
종료 조건(Base Case): 더 이상 재귀 호출을 하지 않아야 할 때 즉시 함수 종료예외 처리: 음수 입력, 0, 타입 오류 등 잘못된 입력을 막기 위해 사용불필요한 계산 방지: 조건이 충족되면 그 시점에서 미리 반환하여 성능 개선
📖 문법, 구문(syntax):
def 함수이름(매개변수):
if 조기종료조건: # 종료 조건 또는 예외 처리
return # 여기서 함수 종료
# 아래는 조건이 충족되지 않을 때만 실행됨
return 재귀호출 또는 결과
◽ 팩토리얼 재귀 함수에서의 조기 리턴이란?
n == 1 일 때 더 이상 재귀 호출을 하지 않고 즉시 1을 반환하는 동작을 말합니다.
-
팩토리얼은
n × (n-1) × ... × 1로 계산되는데,
재귀 함수에서는 이 곱셈을 계속 자기 자신을 부르며 계산합니다. -
하지만 계속 부르기만 하면 무한 호출이 되므로,
n == 1일 때 더 이상 호출하지 않고 바로결과(1)를 리턴합니다. -
이처럼 재귀 호출을 멈추는 조건과 동시에 즉시 결과를 반환하는 것이
조기 리턴(Early Return)입니다.
</> 예시코드: 팩토리얼 재귀 함수에서의 조기 리턴
def factorial(n):
if n == 1: # 조기 리턴 조건 (Base Case)
return 1 # 더 이상 호출하지 않음
return n * factorial(n - 1)# 자기 자신을 호출하면서 누적 곱셈 수행
print("5! =", factorial(5))
- 여기서
if n == 1: return 1이 부분이 바로 조기 리턴입니다.
🖨️ 출력결과:
5! = 120
🔍해설:
def factorial(n): 팩토리얼을 계산하는 함수 -> 5! = 5 × 4 × 3 × 2 × 1
if n == 1: 재귀함수가 자기자신을 호출하다 멈춰야 하는 지점
return 1: 함수 실행을 여기서 즉시 멈추고 1을 돌려주는 부분입니다.
return n * factorial(n - 1): 재귀 호출 부분입니다.
📝 문제1] 팩토리얼의 조기 리턴
factorial() 함수를 완성하세요.
단, n == 1일 때 더 이상 재귀 호출하지 않고 1을 반환해야 합니다.
🖨️ 출력결과:
3! = 6
✅ 정답 코드:
def factorial(n):
if n == 1: # 조기 리턴 조건
return 1
return n * factorial(n - 1) # 재귀 호출
print("3! =", factorial(3))
🔍 해설:
factorial(3)호출 시 →3 * factorial(2)factorial(2)→2 * factorial(1)factorial(1)에서 조기 리턴이 발생 →1반환- 따라서
3 * 2 * 1 = 6출력됨
📝 문제2] 조기 리턴 조건이 없으면 어떤 일이 벌어질까?
다음 코드에서 조기 리턴 조건 if n == 1:을 제거하면 어떤 문제가 발생할까요? 아래의 코드를 수정하여 정상 출력되도록 조기 리턴을 추가하세요.
🖨️ 출력결과:
4! = 24
✅ 정답 코드:
def factorial(n):
if n == 1: # 조기 리턴 조건이 반드시 있어야 함
return 1
return n * factorial(n - 1)
print("4! =", factorial(4))
🔍 해설:
- 재귀 함수는 멈추는 조건(Base Case)이 없으면
계속 자기 자신을 호출하여 무한 반복에 빠지고RecursionError가 발생합니다. if n == 1: return 1은 종료 조건이자 결과 반환 지점으로,
함수 실행 흐름을 끊고 최종 값을 전달해주는 조기 리턴의 핵심입니다.
📝 문제3] 사용자로부터 숫자를 입력받아 팩토리얼 계산하기
n!을 계산하는 팩토리얼 함수를 작성하고, 사용자에게 정수를 입력받아 결과를 출력하세요. 단, n == 1일 때는 조기 리턴으로 재귀 호출을 중단해야 합니다.
🖨️ 출력결과:
5! = 120
✅ 정답 코드:
def factorial(n):
if n == 1:
return 1
return n * factorial(n - 1)
num = int(input("정수를 입력하세요: "))
print(f"{num}! =", factorial(num))
🔍 해설:
- 사용자에게 입력받은 값을 기반으로 팩토리얼을 계산합니다.
factorial(n)함수는 조기 리턴을 이용해n == 1에서 호출을 멈추고
그 값을 위로 거슬러 올라가며 곱셈을 누적합니다.- 예를 들어
5입력 시 →5 * 4 * 3 * 2 * 1=120출력됩니다.
◽ 입력값 유효성 검사로 조기 리턴
조기 리턴은 단지 계산을 끝내기 위한 조건뿐만 아니라, 잘못된
입력값(예외 상황)을 차단할 때도 사용됩니다.
특히 재귀 함수는 조건 없이 계속 호출되면 오류(무한 루프)가 발생할 수 있으므로, 입력값이 유효하지 않으면 아예 처음부터 함수 실행을 멈추는 것이 안전합니다.
</> 예시코드:
def factorial(n):
if n < 1:
print("양의 정수만 입력하세요.")
return None # 조기 종료
if n == 1:
return 1
return n * factorial(n - 1)
factorial(-3)
🔍 해설:
if n < 1 : 사용자가 0 또는 음수를 입력하면 더 이상 계산하지 않고 중단
print(...) : 사용자에게 문제를 알림
return None : 함수를 조기에 종료시킴 (결과값 없음)
if n == 1 : 정상적인 종료 조건 (팩토리얼 계산을 위한 base case)
return n * factorial(n - 1) : 재귀적으로 계산 수행
🖨️ 출력 결과:
양의 정수만 입력하세요.
💬 보충설명: 왜 중요한가요?
- 함수가 무한히 호출되지 않게 막아줍니다.
- 사용자 실수로 프로그램이 멈추는 것을 방지합니다.
- 함수의 안정성(safety)과 신뢰성을 높여줍니다.
📝 문제1] 음수 입력 시 함수 실행 중단 사용자가 입력한 수가 음수이면, “0 이상의 정수만 입력하세요.”라는 문구를 출력하고 함수를 즉시 종료(return)하도록 작성하세요.
🖨️ 출력 결과:
0 이상의 정수만 입력하세요.
✅ 정답 코드:
def say_number(n):
if n < 0:
print("0 이상의 정수만 입력하세요.")
return
print("입력한 숫자:", n)
say_number(-5)
🔍 해설:
if n < 0:조건에서 유효하지 않은 입력값(음수)일 경우 경고 메시지를 출력하고 함수 종료.return을 사용해 함수 실행을 조기에 멈추는 조기 리턴.- 유효한 값이 아닌 경우에는 출력도 하지 않고 깔끔히 종료됩니다.
📝 문제2] 팩토리얼 함수에 유효성 검사 추가
팩토리얼 함수에 양의 정수인지 확인하는 코드를 추가하고,
음수를 입력하면 계산하지 않고 경고 메시지를 출력하세요.
🖨️ 출력 결과:
양의 정수만 입력하세요.
✅ 정답 코드:
def factorial(n):
if n < 1:
print("양의 정수만 입력하세요.")
return None
if n == 1:
return 1
return n * factorial(n - 1)
factorial(5)
🔍 해설:
if n < 1:→ 잘못된 입력값을 확인하는 유효성 검사return None으로 함수 조기 종료- 재귀 함수에서 잘못된 값이 입력되면 무한 호출 방지를 위해 반드시 필요한 구조
📝 문제3] 입력값이 정수가 아닐 경우 조기 리턴
사용자가 입력한 값이 정수가 아니거나 0 이하일 경우,
팩토리얼 계산을 하지 말고 에러 메시지를 출력한 후 함수 실행을 멈추는 함수를 작성하세요.
🖨️ 출력 결과:
양의 정수만 입력하세요.
✅ 정답 코드:
def factorial(n):
if not isinstance(n, int) or n < 1:
print("양의 정수만 입력하세요.")
return None
if n == 1:
return 1
return n * factorial(n - 1)
factorial("abc") # 문자열 입력
factorial(0) # 0 입력
🔍 해설:
if not isinstance(n, int) or n < 1:는
정수가 아닌 값 또는 0 이하의 값을 입력한 경우를 걸러냄return None은 함수 실행을 조기에 중단하여
계산이 진행되지 않도록 막는 안전장치- 실무에서 외부 입력을 받는 경우,
입력값 검증을 통해 오류를 미리 방지하는 습관이 매우 중요
◽ 피보나치 수열에서의 조기 리턴
피보나치 수열 재귀 함수에서도 조기 리턴은 필수 요소입니다.
조기 리턴이 없다면 함수가 무한히 자기 자신을 호출하다가
`RecursionError`(최대 재귀 깊이 초과)가 발생할 수 있습니다.
다시 말해서, 재귀함수에서 멈추는 조건이 없으면 오류를 낸다는 뜻입니다.
그 오류 이름이 RecursionError입니다. 재귀 호출을 너무 많이 해서 멈췄어요!
</> 예시코드: 그래서 "조기 리턴"이 필요해요!
def fib(n):
if n <= 0: # ❌ 잘못된 입력이므로 함수를 조기에 종료
print("양의 정수만 입력하세요.")
return None # 예외 입력 차단용 조기 리턴
if n == 1 or n == 2: # 종료 조건 (Base Case)
return 1
return fib(n - 1) + fib(n - 2)
fib(-3)
if n <= 0:
n이 0 이하인 경우는 피보나치 수열의 정의에 맞지 않기 때문에,
재귀 호출을 아예 시작하지 않고 함수 실행을 멈춥니다.- 이 부분이 비정상 입력을 차단하는 조기 리턴입니다.
if n == 1 or n == 2:
n이 1 또는 2이면 피보나치 수열에서 그 값은 항상 1입니다.- 그래서 더 이상 계산하지 않고 바로 1을 반환(return) 합니다.
- 이게 재귀 함수의 종료 조건(Base Case) 입니다.
return fib(n - 1) + fib(n - 2)
- 그 외의 경우에는
fib(n)을fib(n-1)과fib(n-2)의 합으로 계산합니다. - 이 줄에서 자기 자신을 다시 부르는 재귀 호출이 이루어집니다.
🖨️ 출력 결과:
양의 정수만 입력하세요.
📝 문제1] 잘못된 입력일 때 함수 종료하기
음수나 0이 입력되면 "양의 정수만 입력하세요."라는 문구를 출력하고
함수를 실행하지 않고 종료(return) 하도록 fib() 함수를 완성하세요.
🖨️ 출력 결과:
양의 정수만 입력하세요.
✅ 정답 코드:
def fib(n):
if n <= 0:
print("양의 정수만 입력하세요.")
return None
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
fib(0)
🔍 해설:
n <= 0은 비정상 입력을 차단하는 조기 리턴 조건- 유효하지 않은 입력이 들어오면 함수의 재귀 호출을 시작조차 하지 않고 종료
- 오류 없이 안전하게 실행 흐름을 제어할 수 있음
📝 문제2] 정상 입력에 대해 피보나치 수열 계산하기
사용자가 입력한 값이 1 또는 2이면 바로 1을 반환하고,
그 외의 수는 재귀 호출을 통해 피보나치 값을 계산하도록 코드를 완성하세요.
🖨️ 출력 결과:
fib(1) = 1
fib(5) = 5
✅ 정답 코드:
def fib(n):
if n <= 0:
print("양의 정수만 입력하세요.")
return None
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
print("fib(1) =", fib(1))
print("fib(5) =", fib(5))
🔍 해설:
n == 1 or n == 2는 재귀 종료 조건(Base Case) → 더 이상 함수 호출 없이 1을 반환fib(n - 1) + fib(n - 2)는 피보나치 수열의 정의에 따라 이전 두 항의 합으로 계산- 출력 결과
fib(5) = 5는 다음과 같이 계산됨:
fib(5) = fib(4) + fib(3)
fib(4) = fib(3) + fib(2)
📝 문제3] 사용자 입력에 따라 피보나치 값 계산하기 + 예외 처리 포함
사용자로부터 숫자를 입력받아 피보나치 값을 계산하세요.
단, 0 이하 또는 숫자가 아닌 값이 들어오면 "양의 정수만 입력하세요."라는 문구를 출력하고 함수를 종료하도록 만드세요.
🖨️ 출력 결과:
양의 정수만 입력하세요.
fib(6) = 8
✅ 정답 코드:
def fib(n):
if not isinstance(n, int) or n <= 0:
print("양의 정수만 입력하세요.")
return None
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
# 테스트
fib(-5)
fib("abc") # 실행되지 않도록 int로 미리 처리해야 함
print("fib(6) =", fib(6))
🔍 해설:
not isinstance(n, int)는 정수 타입이 아닌 경우 차단n <= 0는 0 이하의 잘못된 수를 차단- 위 조건 중 하나라도 해당되면 재귀 호출 없이 함수 종료
- 사용자 입력의 유효성을 사전에 검사하는 것은 실무에서도 매우 중요한 안전장치
🔹 리스트 평탄화(Flattening) 하는 재귀 함수 만들기
리스트 평탄화(Flattening)란,
중첩된 리스트(nested list)를 하나의 평면 리스트
(one-dimensional list)로 펼치는 작업을 말합니다.
복잡한 계층 구조의 리스트를 단일 리스트로 변환할 때 유용하며,
재귀(recursion)를 사용하면 구조적으로 간결하고 효율적으로
구현할 수 있습니다.
📖 문법, 구문(syntax):
isinstance(item, list) # isinstance(객체, 자료형) -> item이 list 자료형인지 확인한다
# item은 중첩 데이터로 실행하면 하나씩 값들을 가지므로 객체입니다.
📚 용어: 객체는 값(데이터) + 기능(함수)을 함께 가진 실체. 동작까지 할 수 있는 실체가 객체이다. 비유: 차동차(객체) 속성은 색상,브랜드,속도이고 기능은 달린다, 멈춘다, 방향을 튼다. 그것을 모두 포함하고 있으므로 객체입니다.
🧾 파이썬 코드 공식(평탄화 공식)
def flatten(data):
result = []
for item in data:
if isinstance(item, list): # 리스트가 맞니? True
result += flatten(item) # 재귀함수 호출
# result = result + item 평탄화 될때까지 재귀호출
else:
result.append(item) # 리스트로 모두 풀어지면 빈그릇에 append한다.
return result
nested = [1, [2, 3], [4, [5, 6]], 7]
print(flatten(nested))
실행흐름:
1 → 바로 result.append(1)
[2, 3] → flatten([2, 3]) 호출 → [2, 3] 리턴 → result += [2, 3]
[4, [5, 6]] → flatten([4, [5, 6]]) 호출
4 → append(4)
[5, 6] → flatten([5, 6]) 호출 → [5, 6] 리턴 → += [5, 6]
7 → append(7)
🖨️ 출력 결과:
[1, 2, 3, 4, 5, 6, 7]
✔️ 패턴표현(의사코드 pseudocode)
프로그래밍 언어의 문법을 정확히 따르지는 않지만,
사람이 이해하기 쉽게 논리 흐름을 설명한 코드처럼 생긴 글
flatten(data) =
빈 리스트로 시작해서
각 item에 대해
리스트면 flatten(item)을 다시 호출해서 이어 붙이고
아니면 그대로 추가한다
✔️ flatten() 함수 의사코드
함수 flatten(data)
result라는 빈 리스트 생성
data의 각 item에 대해:
만약 item이 리스트이면:
flatten(item)을 호출해서 펼친 결과를 result에 추가
아니면:
item을 result에 추가
result를 반환
✔️ 처음 언어 공부를 할때 헷갈리는 포인트:
result = []는 함수 안에 있는데, 이게 계속 새로 만들어지는지?flatten(item)을 왜 다시 함수 안에서 호출하는지?+=은 왜 쓰는지?append()와 뭐가 다른지?isinstance(item, list)는 무슨 조건인지?- 어디서부터 코딩을 해야 이런 구조가 되는지?
✔️ 코딩 순서와 사고 순서: 코드를 짤 때는 순서를 아래처럼 생각하는 것이 좋습니다.
1️⃣ 목표를 먼저 생각: 리스트를 평탄화(=낱개로 나열)
nested = [1, [2, 3], [4, [5, 6]], 7]
# → [1, 2, 3, 4, 5, 6, 7]
2️⃣ 반복문으로 접근해보기
for item in nested:
print(item)
결과: 1, [2, 3], [4, [5, 6]], 7
→ 여기서 [2, 3], [4, [5, 6]] 같은 "리스트 안의 리스트"가 문제라는 걸 깨닫게 됨.
3️⃣ “리스트 안에 또 리스트가 있으면” 어떻게 꺼내지?
if isinstance(item, list):
# 리스트라면 또 반복해서 안을 꺼내야 한다 → 재귀 사용
else:
# 그냥 숫자면 result에 넣으면 된다
4️⃣ result는 어디 있어야 하나?
→ result = []는 함수 호출마다 새로 만들어야 하니까 함수 안에 있어야 함.
✔️ 그래서 정리하면 코딩 순서는?
1 결과를 저장할 리스트 필요 result = []
2 data를 하나씩 꺼냄 for item in data:
3 리스트인지 확인 if isinstance(item, list):
4 리스트면 다시 flatten 호출 result += flatten(item)
5 아니면 그냥 추가 result.append(item)
6 결과 반환 return result
✔️ 위의 생각대로 순서 따라가기
nested = [1, [2, 3]]
1단계: item = 1 → 숫자니까 result에 추가
2단계: item = [2, 3] → 리스트니까 flatten([2, 3]) 호출
→ flatten 안에서는 again:
item = 2 → 추가
item = 3 → 추가
→ 반환된 [2, 3]을 result += [2, 3]으로 병합
✔️ 시각적으로 정리
flatten([1, [2, 3]]) 호출
├─ 1 → 숫자 → 추가 → result = [1]
└─ [2, 3] → 리스트 → flatten([2, 3]) 호출
├─ 2 → 추가 → [2]
└─ 3 → 추가 → [2, 3] 반환
최종: result = [1] + [2, 3] → [1, 2, 3]
- 함수 내부 코드는 순서가 논리적으로 맞게 짜야 합니다.
result = []는 함수 호출마다 새로 만들어야 하므로 함수 안에 있어야 합니다.for item in data:는 리스트를 꺼내는 기본 구조입니다.isinstance(item, list)는 리스트인지 판별하는 방법입니다.result += flatten(item)은 여러 개를 한꺼번에 더함,append()는 한 개만 추가입니다.
📝 문제1] 2단계 중첩 리스트 평탄화하기
중첩된 리스트 [1, [2, 3], 4]를 재귀 함수를 사용하여 평탄화하세요.
🖨️ 출력 결과:
[1, 2, 3, 4]
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
nested = [1, [2, 3], 4]
print(flatten(nested))
🔍 해설:
- 리스트 안에 리스트가 한 번 중첩되어 있지만,
재귀 호출을 통해 내부 요소들도 꺼내어 한 줄의 리스트로 변환합니다. result += flatten(item)은 내부 리스트 결과를 병합하는 구문입니다.
📝 문제2] 다양한 타입이 섞인 중첩 리스트 평탄화하기
다양한 데이터 타입이 섞인 중첩 리스트 ["a", [1, [2, "b"]], "c"]를 평탄화하세요.
🖨️ 출력 결과:
['a', 1, 2, 'b', 'c']
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
mixed = ["a", [1, [2, "b"]], "c"]
print(flatten(mixed))
🔍 해설:
flatten()함수는 숫자든 문자든 상관없이 리스트인지 아닌지만 판단하여 처리합니다.isinstance(item, list)는 타입 확인을 위한 내장 함수로,
리스트일 경우에만 재귀 호출하여 내부를 계속 탐색합니다.
📝 문제3] 깊이 5 이상 중첩된 리스트 평탄화하기 리스트가 다음과 같이 깊게 중첩되어 있을 때도 정상적으로 평탄화되도록 함수를 작성하세요:
🖨️ 출력 결과:
[1, [2, [3, [4, [5]]]]]
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
deep_nested = [1, [2, [3, [4, [5]]]]]
print(flatten(deep_nested))
🔍 해설:
- 반복문만으로는 깊이가 5단계인 중첩 구조를 처리하기 어렵습니다.
- 재귀는 자기 자신을 계속 호출하므로, 중첩 깊이에 상관없이
가장 안쪽 항목까지 찾아내어 한 줄로 펼칠 수 있습니다. - 이 문제는 재귀의 유연성과 깊이 탐색 능력을 실습하는 대표 예제입니다.
◽ 다양한 타입의 중첩 리스트 평탄화 (문자열 포함)
다양한 타입의 중첩 리스트는 숫자뿐만 아니라 문자열(str),
불린(bool), 기타 객체들이리스트 안에 섞여 있는 구조를 말하며,
이들을 모두 꺼내서 한 줄로 나열하는 것을 말합니다.
</> 예시코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list): # 리스트면 다시 재귀 호출
result += flatten(item) # 평탄화된 결과 병합
else:
result.append(item) # 리스트가 아니면 그대로 추가
return result
mixed = ["a", [1, ["b", True]], [[3.14, False], "c"]]
print(flatten(mixed))
🖨️ 출력 결과:
['a', 1, 'b', True, 3.14, False, 'c']
🔍 해설:
flatten(data)함수는 중첩된 리스트 구조를 하나의 평면 리스트로 펼치는 재귀 함수입니다.mixed리스트에는 문자열("a","b","c"), 정수(1), 부동소수점(3.14), 불린값(True,False)이 리스트 안에 섞여서 중첩되어 있습니다.isinstance(item, list)는 현재 요소가 리스트인지 확인하여,- 리스트일 경우:
flatten(item)을 재귀 호출하여 내부 항목까지 모두 추출하고result += ...로 병합 - 리스트가 아닐 경우: 그대로
append()로 결과 리스트에 추가
- 리스트일 경우:
- 출력 결과는 모든 요소가 평탄화되어 하나의 리스트로 정렬됩니다.
📝 문제1] 문자열과 숫자가 섞인 리스트 평탄화
중첩된 리스트 ["x", [1, 2], "y"]를 평탄화하여 한 줄로 펼치세요.
🖨️ 출력 결과:
['x', 1, 2, 'y']
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
mixed = ["x", [1, 2], "y"]
print(flatten(mixed))
🔍 해설:
- 리스트 내부에
"x",[1, 2],"y"가 있으며,
[1, 2]라는 하위 리스트의 숫자까지 모두 꺼내어 평면 리스트로 나열합니다. isinstance(item, list)로 리스트인지 검사한 후,
리스트면 재귀 호출, 아니면 그대로append()합니다.
📝 문제2] 문자열, 숫자, 불린값이 섞인 리스트 평탄화
다음과 같은 리스트를 평탄화하세요:
["a", [1, ["b", True]], "z"]
🖨️ 출력 결과:
['a', 1, 'b', True, 'z']
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
mixed = ["a", [1, ["b", True]], "z"]
print(flatten(mixed))
🔍 해설:
- 리스트 안에
"a"와"z"라는 문자열,
[1, ["b", True]]라는 2단계 중첩된 리스트가 포함되어 있습니다. - 재귀를 통해
"b"와True까지 꺼내 모든 값을 한 줄로 정렬합니다. - 타입이 어떤 것이든, 리스트인지 여부만 검사하여 처리하는 것이 핵심입니다.
📝 문제3] 실수, 불린, 문자열, 숫자 등 다양한 타입이 섞인 리스트 평탄화
다음 리스트를 평탄화하세요:
[[False], "start", [1.5, ["deep", [True]]], 42]
🖨️ 출력 결과:
[False, 'start', 1.5, 'deep', True, 42]
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
mixed = [[False], "start", [1.5, ["deep", [True]]], 42]
print(flatten(mixed))
🔍 해설:
- 이 리스트에는 불린값(False, True), 문자열("start", "deep"), 실수(1.5), 정수(42)가 다양한 중첩 구조로 섞여 있습니다.
- 깊은 중첩 구조(
[["deep", [True]]])도 재귀를 통해 문제없이 꺼낼 수 있습니다. - 타입이 무엇이든 리스트만 확인하고 재귀 호출하기 때문에 모든 구조에 유연하게 대응 가능합니다.
📝 문제4] 다음과 같은 중첩 리스트 구조가 있습니다. 이 안에는 숫자, 리스트, 그리고 문장(문자열)이 섞여 있습니다.
문장(문자열)은 한 글자씩 쪼개지지 않고, 하나의 데이터로 유지되게 하여 평탄화한 리스트를 만들어 출력해보세요. 그리고 의사코드로 만들어보세요.
data = [1, [2, "Hello world"], [3, [4, "Python is fun"]], 5]
문제조건:
- 리스트 안의 모든 요소를 평탄화하되,
"Hello world"와"Python is fun"같은 문장은 한 항목으로 처리되어야 합니다.- 즉, 문자 단위로 쪼개지면 안 됩니다.
🖨️ 출력 결과:
[1, 2, 'Hello world', 3, 4, 'Python is fun', 5]
✅ 정답 코드:
from collections.abc import Iterable
def flatten(data):
result = []
for item in data:
if isinstance(item, Iterable) and not isinstance(item, (str, bytes)):
result += flatten(item) # 재귀적으로 내부 리스트를 펼침
else:
result.append(item) # 숫자나 문자열은 그대로 추가
return result
data = [1, [2, "Hello world"], [3, [4, "Python is fun"]], 5]
print(flatten(data))
✔️ 의사코드
함수 flatten(데이터):
결과 리스트를 빈 상태로 만든다
데이터의 각 항목에 대해:
만약 항목이 반복 가능한 자료형(Iterable)이면서 문자열은 아닐 경우:
그 항목을 flatten 함수로 다시 호출해서 결과에 이어 붙인다
그렇지 않으면:
결과 리스트에 항목을 그대로 추가한다
결과 리스트를 반환한다
🔍 해설:
- 이 문제의 핵심은
"Hello world"와 같은 문자열을 한 글자씩 쪼개지 않고,
하나의 덩어리로 처리해야 한다는 점입니다. - 파이썬에서 문자열은
Iterable로 인식되기 때문에,
그냥isinstance(item, Iterable)조건만 쓰면"Hello world"도'H', 'e', 'l'...로 쪼개지게 됩니다. - 따라서 문자열은 제외시켜야 하므로
not isinstance(item, (str, bytes))조건을 추가합니다. - 이 조건이 있으면 문자열은 그대로
append()되어 하나의 문장으로 유지됩니다.
◽ 반복문으로 처리할 수 없는 깊이의 리스트도 재귀로 해결 가능
반복문(for, while)은 리스트를 순서대로 처리할 수 있지만,
중첩의 깊이(리스트 안에 리스트가 몇 겹으로 들어 있는지)가 정해져
있지 않거나 너무 깊어지면 반복문만으로는 처리하기 어려운 한계가
있습니다.
반면, 재귀 함수(recursive function)는 자기 자신을 계속 호출하면서
내부 구조를 탐색하므로 리스트가 몇 번 중첩되었든 깊이에 상관없이
끝까지 내려가 처리할 수 있습니다.
</> 예시코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list): # 리스트면 재귀 호출
result += flatten(item) # 결과 리스트에 병합
else:
result.append(item) # 리스트가 아니면 그대로 추가
return result
deep_nested = [1, [2, [3, [4, [5]]]]]
# 깊이가 5단계나 되는 중첩 리스트
print(flatten(deep_nested))
🖨️ 출력 결과:
[1, 2, 3, 4, 5]
🔍 해설:
deep_nested는 리스트 안에 리스트가 또 있고… 총 5단계로 중첩된 구조입니다.- 반복문만 사용하면 몇 단계인지 미리 알아야 하고,
그에 맞게for문을 여러 번 중첩해야 처리할 수 있습니다.
❌ 반복문만으로 처리할 경우:
# 깊이를 알아야 가능한 코드 (비효율적)
for i in deep_nested:
for j in i:
for k in j:
...
하지만 flatten() 함수는 재귀(recursion)를 이용해,
- 현재 항목이 리스트인지 확인
- 리스트면 다시 자기 자신을 호출
- 계속 깊은 곳까지 들어가서 마지막 값까지 꺼냄
- 리스트가 아닌 값은 그대로 결과에 추가 그 결과, 몇 단계든 상관없이 다음처럼 평평한 리스트로 만들어 줍니다:
📝 문제1] 얕은 중첩 리스트를 평탄화하기
중첩된 리스트 [1, [2, 3], 4]를 재귀 함수로 평탄화하여 한 줄의 리스트로 출력하세요.
🖨️ 출력 결과:
[1, 2, 3, 4]
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
example = [1, [2, 3], 4]
print(flatten(example))
🔍 해설:
- 이 문제는 중첩이 1단계만 있는 리스트입니다.
- 반복문으로도 처리 가능하지만,
flatten()은 리스트인지 확인하고 재귀 호출을 통해 더 유연하게 처리할 수 있습니다. - 구조적으로 더 깊은 중첩도 처리할 수 있도록 기반을 익히는 단계입니다.
📝 문제2] 반복문으로는 불가능한 5단계 중첩 리스트 평탄화
다음과 같은 깊은 중첩 리스트를 평탄화하세요: [1, [2, [3, [4, [5]]]]]
🖨️ 출력 결과:
[1, 2, 3, 4, 5]
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
deep_nested = [1, [2, [3, [4, [5]]]]]
print(flatten(deep_nested))
🔍 해설:
- 리스트가 무려 5단계로 중첩되어 있어 반복문만으로는 불가능에 가깝습니다.
flatten()은 리스트인지 확인하면서 자기 자신을 계속 호출하는 재귀 함수이므로 중첩 깊이에 상관없이 끝까지 내려가서 모든 요소를 추출할 수 있습니다.
📝 문제3] 문자열, 불린, 실수 등이 섞인 깊은 중첩 리스트 평탄화 다음 리스트를 재귀적으로 평탄화하여 다양한 타입의 데이터를 하나의 리스트로 출력하세요:
[True, [1.2, ["deep", [False, [100]]]], "end"]
🖨️ 출력 결과:
[True, 1.2, 'deep', False, 100, 'end']
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
complex_nested = [True, [1.2, ["deep", [False, [100]]]], "end"]
print(flatten(complex_nested))
🔍 해설:
- 이 리스트는 불린, 실수, 문자열, 정수 등 다양한 타입이 섞여 있고
중첩도 4단계 이상으로 깊습니다. - 반복문만으로는 처리할 수 없지만,
flatten()은 타입에 관계없이
리스트만 재귀적으로 처리하기 때문에 유연하게 평탄화할 수 있습니다. - 실무에서도 복잡한 데이터(JSON, 로그 트리 등)를 다룰 때 유용한 구조입니다.
🔹 함수 복습
1️⃣ 함수, 매개변수, 인자, 반환값, 리턴문
</> 예시 코드
def format_report(title, *items):
report = f"{title} 보고서\n"
report += "\n".join([f"- {i + 1}. {item}" for i, item in enumerate(items)])
return report # 반환값
daily = format_report("일일 업무", "DB 점검", "API 테스트", "오류 보고서 제출")
print(daily)
✔️ 의사코드
함수 format_report(제목, 여러 개의 항목들):
1. "제목 + ' 보고서\n'" 형식의 문자열을 만든다 → report 변수에 저장
2. 항목들을 하나씩 반복하면서:
- 항목 앞에 번호를 붙여 문자열을 만든다
형식: "- 번호. 항목내용"
예: "- 1. DB 점검"
3. 항목 문자열들을 줄바꿈(\n)으로 이어 붙인다
4. report 문자열에 항목 문자열들을 덧붙인다
5. 최종적으로 report를 반환한다
함수 호출: format_report("일일 업무", "DB 점검", "API 테스트", "오류 보고서 제출")
→ 반환값을 daily 변수에 저장
daily를 출력한다
🖨️ 출력 결과
일일 업무 보고서
- 1. DB 점검
- 2. API 테스트
- 3. 오류 보고서 제출
title은 매개변수,"일일 업무"는 인자*items로 여러 업무 항목을 받고, 이를 가공한 문자열을 반환
2️⃣ 기본값 매개변수 (default parameter)
</> 예시 코드
def create_user(name, role="user", active=True):
return f"{name} | 권한: {role} | 활성화 상태: {'ON' if active else 'OFF'}"
print(create_user("이지은"))
print(create_user("김민재", role="admin", active=False))
✔️ 의사코드
함수 create_user(이름, 역할="user", 활성화여부=True):
1. 문자열을 생성한다:
- "{이름} | 권한: {역할} | 활성화 상태: ON 또는 OFF" 형식
- 활성화 상태가 True면 'ON', False면 'OFF'를 표시한다
1. 이 문자열을 반환한다 return
함수 호출 1: 첫번째 print문
create_user("이지은")
→ 역할은 기본값 "user"
→ 활성화 상태는 기본값 True
→ 출력: "이지은 | 권한: user | 활성화 상태: ON"
함수 호출 2:
create_user("김민재", 역할="admin", 활성화여부=False)
→ 출력: "김민재 | 권한: admin | 활성화 상태: OFF"
🖨️ 출력 결과
이지은 | 권한: user | 활성화 상태: ON
김민재 | 권한: admin | 활성화 상태: OFF
- 매개변수
role과active는 기본값을 가짐 - 인자를 생략하면 자동으로 기본값이 적용됨
3️⃣ 키워드 인자 (keyword argument)
</> 예시 코드
def send_email(subject, sender, receiver, body):
print(f"[{subject}]\n보낸 사람: {sender}\n받는 사람: {receiver}\n내용: {body}\n")
send_email(receiver="team@company.com",
sender="admin@company.com",
subject="회의 일정 변경",
body="회의 시간이 오후 3시로 변경되었습니다.")
✔️ 의사코드
함수 send_email(제목, 보낸사람, 받는사람, 본문내용):
1. 다음 형식의 메시지를 화면에 출력한다:
[제목]
보낸 사람: 보낸사람
받는 사람: 받는사람
내용: 본문내용
함수 호출:
인자를 이름으로 지정하여 전달한다 (키워드 인자 방식)
제목: "회의 일정 변경"
보낸사람: "admin@company.com"
받는사람: "team@company.com"
본문내용: "회의 시간이 오후 3시로 변경되었습니다."
실행 결과:
[회의 일정 변경]
보낸 사람: admin@company.com
받는 사람: team@company.com
내용: 회의 시간이 오후 3시로 변경되었습니다.
🖨️ 출력 결과
[회의 일정 변경]
보낸 사람: admin@company.com
받는 사람: team@company.com
내용: 회의 시간이 오후 3시로 변경되었습니다.
- 인자 순서를 무시하고, 키 이름으로 명확하게 전달 가능
- 실무에서 가독성과 명확성 확보에 유리
4️⃣ 가변 인자 (*args)
</> 예시 코드
def multiply_chain(factor, *numbers):
result = [factor * num for num in numbers if isinstance(num, (int, float))]
return result
print(multiply_chain(3, 10, "hi", 4.5, None))
✔️ 의사코드
함수 multiply_chain(곱할값, 여러 개의 숫자들):
1. 결과 리스트를 만든다:
- 숫자 목록 중에서 정수(int) 또는 실수(float)인 항목만 골라서(조건문)
- 각 항목에 곱할값을 곱한 결과를 리스트로 만든다 (참인값들만)
2. 결과 리스트를 반환한다
함수 호출:
multiply_chain(3, 10, "hi", 4.5, None)
→ 곱할값: 3
→ 숫자들: 10, "hi", 4.5, None
→ 숫자인 값만 추림: 10, 4.5
→ 계산: 10 * 3 = 30, 4.5 * 3 = 13.5
→ 결과 리스트: [30, 13.5]
출력 결과:
[30, 13.5]
🖨️ 출력 결과
[30, 13.5]
- 여러 타입이 혼합된 인자 중 숫자만 골라 3배 곱한 리스트 반환
*args는 필터링 및 반복 처리에 매우 유용함
5️⃣ 가변 키워드 인자 (**kwargs)
</> 예시 코드
def make_html_tag(tag, **attributes):
attr_string = " ".join([f'{k}="{v}"' for k, v in attributes.items()])
return f"<{tag} {attr_string}></{tag}>"
print(make_html_tag("button", type="submit", class_="btn btn-primary", disabled="true"))
✔️ 의사코드
함수 make_html_tag(태그이름, 여러 개의 속성들=키워드 인자):
1. 속성 딕셔너리에서 각 키-값 쌍을 꺼내어
문자열 형식 '키="값"'으로 만든다
2. 만들어진 속성 문자열들을 공백으로 연결해서 하나의 문자열로 만든다
예: 'type="submit" class_="btn btn-primary" disabled="true"'
3. 최종적으로 HTML 태그 형식으로 반환한다:
형식: <태그이름 속성문자열></태그이름>
함수 호출:
make_html_tag("button", type="submit", class_="btn btn-primary", disabled="true")
→ 태그 이름: "button"
→ 속성들:
- type="submit"
- class_="btn btn-primary"
- disabled="true"
→ 반환 결과:
<button type="submit" class_="btn btn-primary" disabled="true"></button>
출력:
<button type="submit" class_="btn btn-primary" disabled="true"></button>
🖨️ 출력 결과
<button type="submit" class_="btn btn-primary" disabled="true"></button>
**kwargs를 활용해 태그 속성을 유동적으로 처리- 실전에서는 HTML 템플릿 렌더링, 데이터 변환 등에 자주 사용됨
6️⃣ 클로저 (closure)
</> 예시 코드
def score_tracker(start=0):
score = start
def update(points):
nonlocal score
score += points
return score
return update
game_score = score_tracker(10)
print(game_score(5)) # 15
print(game_score(10)) # 25
✔️ 의사코드
함수 score_tracker(초기점수=0):
내부 변수 score에 초기점수를 저장한다
내부 함수 update(점수):
score 값을 전달받은 점수만큼 증가시킨다 score += points
업데이트된 score를 반환한다 return
update 함수를 반환한다 (함수 자체를 리턴함) return
game_score = score_tracker(10)
→ score = 10으로 시작하는 update 함수를 game_score라는 이름으로 저장
game_score(5)
→ score = 10 + 5 → 15 반환
game_score(10)
→ score = 15 + 10 → 25 반환
🖨️ 출력 결과
15
25
update()는score_tracker()의 지역변수score를 기억- 함수 내부 상태를 은밀히 유지하면서 조작하는 함수 → 클로저
7️⃣ 고차 함수 (Higher-Order Function)
</> 예시 코드
def apply_to_even(func, data):
return [func(x) for x in data if x % 2 == 0]
def square(x): return x ** 2
numbers = [1, 2, 3, 4, 5, 6]
print(apply_to_even(square, numbers))
✔️ 의사코드
함수 apply_to_even(함수, 데이터리스트):
1. 데이터리스트에서 짝수인 값만 골라낸다
2. 골라낸 짝수 각각에 대해 전달받은 함수를 적용한다
3. 그 결과를 리스트로 만들어 반환한다
함수 square(x):
x의 제곱 값을 반환한다
리스트 numbers = [1, 2, 3, 4, 5, 6]
apply_to_even(square, numbers) 실행:
- 짝수만 필터링: 2, 4, 6
- square 함수 적용:
→ square(2) → 4
→ square(4) → 16
→ square(6) → 36
- 최종 결과 리스트: [4, 16, 36]
출력 결과:
[4, 16, 36]
🖨️ 출력 결과
[4, 16, 36]
apply_to_even()은 함수func를 인자로 받아 짝수에만 적용- 함수가 함수를 받아서 처리하는 구조 → 고차 함수
✅ 전체 정리 요약표
| 개념 | 활용도 | 설명 |
|---|---|---|
| 기본 함수 구성 | 필수 | 함수 정의, 매개변수, 인자, 리턴 |
| 기본값 매개변수 | 자주 | 선택적 동작 제어 |
| 키워드 인자 | 자주 | 순서 없이 명확하게 인자 전달 |
*args |
자주 | 유동적인 위치 인자 처리 |
**kwargs |
자주 | 유동적인 키워드 인자 처리 |
| 클로저 | 고급 | 상태를 기억하는 함수 |
| 고차 함수 | 고급 | 함수 조합, 동작 추상화 가능 |
💭직접 풀어보세요.
📝 문제1] 재귀로 1부터 n까지 합 구하기
숫자 n이 주어지면, 1 + 2 + ... + n까지의 합을 재귀 함수로 계산하세요.
단, n <= 0인 경우 함수 실행을 조기 종료하고 안내 문구를 출력하세요.
🖨️ 출력 결과:
1부터 5까지의 합: 15
✅ 정답 코드:
def sum_recursive(n):
if n <= 0:
print("양의 정수를 입력하세요.")
return None
if n == 1:
return 1
return n + sum_recursive(n - 1)
print("1부터 5까지의 합:", sum_recursive(5))
🔍 해설:
n <= 0은 유효성 검사 → 조기 리턴n == 1은 종료 조건 (Base Case)- 이 구조는 팩토리얼 구조와 비슷한 누적 합 계산 재귀 예제입니다.
📝 문제2] 메모화(Memoization)로 피보나치 수열 최적화
기본 재귀 방식으로 피보나치 수열을 구현하면 중복 계산이 많아집니다.
이를 메모화를 활용해 최적화하세요.
🖨️ 출력 결과:
fib(10) = 55
✅ 정답 코드:
memo = {}
def fib(n):
if n <= 0:
return 0
if n == 1 or n == 2:
return 1
if n in memo:
return memo[n]
memo[n] = fib(n - 1) + fib(n - 2)
return memo[n]
print("fib(10) =", fib(10))
🔍 해설:
memo딕셔너리에 계산된 결과를 저장하여 중복 호출 방지fib(10)을 처음 계산할 때만 수행되고, 이후엔 저장된 값 사용- 실무에서 성능 향상이 중요한 알고리즘 문제에 자주 활용
📝 문제3] 중첩 리스트에서 문자열만 추출하여 평탄화하기 다음 리스트에서 문자열만 추출해 평탄화된 문자열 리스트를 출력하는 함수를 작성하세요.
🖨️ 출력 결과:
['a', 'b', 'hello']
✅ 정답 코드:
def flatten_strings(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten_strings(item)
elif isinstance(item, str):
result.append(item)
return result
mixed = ["a", [1, ["b", True]], [[3.14], "hello"]]
print(flatten_strings(mixed))
🔍 해설:
- 리스트 내부에서 문자열만 골라서 추출
- 재귀를 통해 모든 중첩 구조를 순회
elif isinstance(item, str)조건으로 타입 필터링
📝 문제4] 리스트 안의 정수 합 구하기 (중첩 포함) 리스트 안에 중첩된 구조가 있어도, 내부의 정수만 찾아 모두 합산하는 재귀 함수를 만드세요.
🖨️ 출력 결과:
합계: 21
✅ 정답 코드:
def sum_nested(data):
total = 0
for item in data:
if isinstance(item, list):
total += sum_nested(item)
elif isinstance(item, int):
total += item
return total
nested = [1, [2, [3, "a"], 4], [5, [6]], "end"]
print("합계:", sum_nested(nested))
🔍 해설:
- 리스트 안의 정수만 조건 검사하여 합산
- 재귀로 깊은 구조도 탐색 가능
- 실무에서 JSON처럼 복합 데이터 구조를 정리하거나 분석할 때 자주 사용
📝 문제5] 재귀 호출 회수 추적하기 (카운터 포함)
재귀 호출이 몇 번 발생했는지 추적하면서 피보나치 수열을 계산하세요.
(단, n <= 0일 경우 조기 종료)
🖨️ 출력 결과:
호출 횟수: 19
fib(5) = 5
✅ 정답 코드:
call_count = 0
def fib(n):
global call_count
if n <= 0:
print("양의 정수만 입력하세요.")
return None
call_count += 1
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
result = fib(5)
print("호출 횟수:", call_count)
print("fib(5) =", result)
🔍 해설:
call_count로 재귀 호출 횟수를 기록- 재귀가 얼마나 많은 중복 호출을 야기하는지 시각적으로 확인 가능
- 이 구조는 이후 메모화의 필요성을 설명할 때 매우 유용
📝 문제6] 중첩 리스트에서 숫자와 문자열을 각각 분리하여 출력
리스트에 다양한 타입이 섞여 있는 경우,
숫자와 문자열만 분리하여 각각 별도의 리스트로 반환하세요
🖨️ 출력 결과:
숫자: [1, 2, 3]
문자: ['a', 'b']
✅ 정답 코드:
def separate(data):
numbers = []
strings = []
for item in data:
if isinstance(item, list):
sub_numbers, sub_strings = separate(item)
numbers += sub_numbers
strings += sub_strings
elif isinstance(item, int):
numbers.append(item)
elif isinstance(item, str):
strings.append(item)
return numbers, strings
nested = [1, "a", [2, ["b", 3]]]
nums, strs = separate(nested)
print("숫자:", nums)
print("문자:", strs)
🔍 해설:
- 리스트 내 아이템을 숫자/문자별로 분류하여 각 리스트에 저장
- 재귀 호출을 통해 중첩 리스트도 문제없이 탐색
- 실무에서 입력값 정제, 필터링, 시각화 전처리 등 다양한 곳에서 사용됨
📝 문제7] 부터 n까지 짝수만 출력하기 (재귀 + 조기 리턴)
재귀 함수를 사용하여 1부터 n까지 중 짝수만 출력하세요.
단, n이 0 이하일 경우 “양의 정수만 입력하세요.” 라고 출력하고 함수를 종료하세요.
🖨️ 출력 결과:
2
4
6
✅ 정답 코드:
def print_even(n):
if n <= 0:
print("양의 정수만 입력하세요.")
return
if n == 1:
return
print_even(n - 1)
if n % 2 == 0:
print(n)
print_even(6)
🔍 해설:
n <= 0조기 리턴으로 예외 차단n == 1은 종료 조건- 재귀적으로 1부터 n까지 증가하며 짝수만 필터링 출력
📝 문제8] 메모화 없이 피보나치 호출 횟수 출력하기 재귀로 피보나치 수열을 구할 때 재귀 호출이 몇 번 일어나는지 카운트하세요.
🖨️ 출력 결과:
fib(5) = 5
재귀 호출 횟수: 15
✅ 정답 코드:
counter = 0
def fib(n):
global counter
counter += 1
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
print("fib(5) =", fib(5))
print("재귀 호출 횟수:", counter)
🔍 해설:
- 피보나치 수열은 중복 호출이 많아져 성능 저하 발생
- 호출 횟수를 출력해보고 나중에 메모화의 필요성을 설명하는 기반이 됨
📝 문제9] 다양한 타입의 리스트에서 숫자만 추출하기 다양한 타입이 섞인 중첩 리스트에서 숫자(int, float)만 추출해서 한 리스트에 담으세요.
🖨️ 출력 결과:
[1, 2.5, 3, 4.0]
✅ 정답 코드:
def extract_numbers(data):
result = []
for item in data:
if isinstance(item, list):
result += extract_numbers(item)
elif isinstance(item, (int, float)):
result.append(item)
return result
mixed = [1, ["a", 2.5], ["b", [3, "x"], [4.0]]]
print(extract_numbers(mixed))
🔍 해설:
isinstance(item, (int, float))→ 숫자만 추출- 재귀 구조로 모든 깊이까지 탐색
- 실무 데이터 정제(숫자 필터링) 작업에 자주 사용됨
📝 문제10] 중첩 리스트에서 가장 깊은 값 반환하기
다음 리스트에서 가장 안쪽에 있는 값을 찾아 반환하는 재귀 함수를 작성하세요. 단, 리스트 구조는 항상 [...[[value]]] 형태로 주어집니다.
🖨️ 출력 결과:
가장 깊은 값: 999
✅ 정답 코드:
def get_deepest(data):
if isinstance(data, list) and len(data) == 1:
return get_deepest(data[0])
return data
nested = [[[[[[999]]]]]]
print("가장 깊은 값:", get_deepest(nested))
🔍 해설:
- 깊이가 몇 겹이든, 리스트 안에 리스트가 하나씩만 있을 때 마지막 값을 추적
- 반복문으로는 불가능에 가까운 구조 → 재귀가 적합
- 실무에서는 트리 구조나 JSON 깊은 필드 추적 등에 응용됨
📝 문제11] 리스트 안의 문자열 길이 합계 구하기 중첩 리스트 안에 있는 모든 문자열의 총 길이 합을 구하세요.
🖨️ 출력 결과:
총 문자 수: 10
✅ 정답 코드:
def total_string_length(data):
total = 0
for item in data:
if isinstance(item, list):
total += total_string_length(item)
elif isinstance(item, str):
total += len(item)
return total
nested = ["hi", ["abc", ["de", ["xyz"]]]]
print("총 문자 수:", total_string_length(nested))
🔍 해설:
- 재귀로 리스트를 탐색하며 문자열의 길이만 누적
len(item)으로 문자열 길이를 계산- 실무에서 텍스트 분석, UI 표시 최적화 등에서 활용
📝 문제12] 재귀적으로 HTML 태그 깊이 확인하기 HTML 구조가 리스트로 표현되어 있을 때, 태그가 몇 단계까지 중첩되어 있는지(깊이)를 계산하세요.
🖨️ 출력 결과:
최대 깊이: 4
✅ 정답 코드:
def get_depth(data):
if not isinstance(data, list):
return 0
return 1 + max(get_depth(item) for item in data)
html_structure = ["<div>", ["<section>", ["<article>", ["<p>"]]]]
print("최대 깊이:", get_depth(html_structure))
🔍 해설:
- 리스트의 중첩 구조를 이용해 중첩 깊이(재귀 깊이)** 측정
- HTML 같은 중첩된 데이터 구조를 처리할 때 자주 사용되는 패턴
- 실무에서 DOM 구조 분석, XML/JSON 구조 탐색 등에 활용
📝 문제13] 1부터 n까지 홀수만 출력하기 (재귀 + 조건 분기)
재귀 함수를 사용하여 1부터 n까지 중 홀수만 출력하세요.
단, n이 0 이하일 경우 **"양의 정수만 입력하세요."**를 출력하고 함수 실행을 중단하세요.
🖨️ 출력 결과:
1
3
5
✅ 정답 코드:
def print_odd(n):
if n <= 0:
print("양의 정수만 입력하세요.")
return
if n > 1:
print_odd(n - 1)
if n % 2 == 1:
print(n)
print_odd(5)
🔍 해설:
- 재귀 호출 전에
print_odd(n - 1)을 먼저 실행하여 1부터 순차적으로 출력 - 홀수만 출력 조건은
if n % 2 == 1 - 입력값 유효성 검사 + 조기 리턴 포함
📝 문제14] 피보나치 수열의 항들 나열하기 (조기 리턴 + 반복 출력)
n을 입력받아 1부터 n번째 피보나치 수까지 출력하는 프로그램을 작성하세요.
단, n이 0 이하이면 조기 종료하세요.
🖨️ 출력 결과:
1 1 2 3 5
✅ 정답 코드:
def fib(n):
if n <= 0:
return None
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
def print_fib_sequence(n):
if n <= 0:
print("양의 정수만 입력하세요.")
return
for i in range(1, n + 1):
print(fib(i), end=' ')
print_fib_sequence(5)
🔍 해설:
- 피보나치 수열의 계산은
fib(n)으로 재귀 수행 - 조기 리턴을 통해 입력값 검사
- 출력은
for반복문으로 수행 → 반복과 재귀의 혼합
📝 문제15] 중첩 리스트에서 실수(float)만 추출하여 평탄화하기 아래와 같은 중첩 리스트에서 **실수(float)**만 골라 한 줄의 리스트로 출력하세요.
🖨️ 출력 결과:
[1.5, 2.2, 3.3]
✅ 정답 코드:
def extract_floats(data):
result = []
for item in data:
if isinstance(item, list):
result += extract_floats(item)
elif isinstance(item, float):
result.append(item)
return result
nested = [1.5, ["a", [2.2, "b", [3.3]]], "x"]
print(extract_floats(nested))
🔍 해설:
- 재귀적으로 리스트를 탐색하면서 타입 필터링
isinstance(item, float)로 실수만 추출- 리스트 병합은
+=연산으로 평탄화
📝 문제16] 리스트에서 가장 큰 정수 찾기 (중첩 포함)
숫자와 리스트가 섞인 구조에서 가장 큰 정수 값을 찾아 반환하세요.
(단, 음수와 양수 혼합 가능)
🖨️ 출력 결과:
최댓값: 99
✅ 정답 코드:
def find_max(data):
max_val = float('-inf')
for item in data:
if isinstance(item, list):
max_val = max(max_val, find_max(item))
elif isinstance(item, int):
max_val = max(max_val, item)
return max_val
nums = [1, [2, [99, -1]], [45]]
print("최댓값:", find_max(nums))
🔍 해설:
- 리스트 안의 모든 정수에 접근
float('-inf')로 초기값 설정 → 실무에서 안전한 초기값 처리 방식- 재귀 호출로 모든 깊이 탐색 가능
📝 문제17] JSON 구조처럼 생긴 중첩 리스트에서 문자열만 평탄화 JSON처럼 문자열이 중첩된 리스트에서 모든 문자열을 꺼내어 하나의 리스트로 반환하세요.
🖨️ 출력 결과:
['name', 'age', 'city', 'country']
✅ 정답 코드:
def extract_strings(data):
result = []
for item in data:
if isinstance(item, list):
result += extract_strings(item)
elif isinstance(item, str):
result.append(item)
return result
json_like = [["name", ["age"]], ["city", ["country"]]]
print(extract_strings(json_like))
🔍 해설:
- 실무에서 JSON 파싱 시 필요한 리스트 평탄화 패턴
- 문자열만 추출하여 데이터 필드 목록 정리 가능
- 재귀의 가장 실용적인 예 중 하나
📝 문제18] 중첩 리스트의 깊이 구하기 리스트가 몇 단계까지 중첩되었는지 재귀를 이용해 중첩 깊이(depth)를 구하세요.
🖨️ 출력 결과:
중첩 깊이: 4
✅ 정답 코드:
def get_depth(data):
if not isinstance(data, list):
return 0
if not data:
return 1
return 1 + max(get_depth(item) for item in data)
nested = [1, [2, [3, [4]]]]
print("중첩 깊이:", get_depth(nested))
🔍 해설:
- 재귀적으로 각 항목의 깊이를 구하고 그 중 최댓값에 +1
- 리스트가 아닌 경우 0, 빈 리스트는 1단계로 처리
- DOM 탐색, JSON 구조 분석, 코드 분석기 등에 유용
📝 문제19] 1부터 n까지 자연수의 곱 구하기 (팩토리얼)
사용자가 입력한 수 n에 대해 1 × 2 × ... × n을 계산하는 팩토리얼 재귀 함수를 작성하세요.
단, n <= 0일 경우 조기 리턴으로 "양의 정수를 입력하세요." 출력 후 종료하세요.
🖨️ 출력 결과:
결과: 120
✅ 정답 코드:
def factorial(n):
if n <= 0:
print("양의 정수를 입력하세요.")
return None
if n == 1:
return 1
return n * factorial(n - 1)
print("결과:", factorial(5))
🔍 해설:
n <= 0조기 리턴은 입력값 유효성 검사n == 1은 종료 조건 (Base Case)- 팩토리얼 구조에 맞는 누적 곱셈 형태의 재귀 구현
📝 문제20] 피보나치 수열에서 메모화 적용하기
기존 피보나치 재귀 함수에 메모화(memoization) 기능을 추가하여
불필요한 중복 호출 없이 fib(10) 값을 구하세요.
🖨️ 출력 결과:
fib(10) = 55
✅ 정답 코드:
memo = {}
def fib(n):
if n <= 0:
return 0
if n == 1 or n == 2:
return 1
if n in memo:
return memo[n]
memo[n] = fib(n - 1) + fib(n - 2)
return memo[n]
print("fib(10) =", fib(10))
🔍 해설:
memo딕셔너리에 이미 계산된 결과 저장 → 중복 계산 제거- 재귀 구조는 유지하면서 성능 개선 효과 큼
- 실무 알고리즘 문제에서 자주 활용됨
📝 문제21] 문자열, 숫자, 불린이 섞인 중첩 리스트 평탄화 다음과 같은 리스트에서 모든 항목을 한 줄의 리스트로 평탄화하세요.
["a", [1, ["b", True]], [[3.14], "z"]]
🖨️ 출력 결과:
['a', 1, 'b', True, 3.14, 'z']
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
mixed = ["a", [1, ["b", True]], [[3.14], "z"]]
print(flatten(mixed))
🔍 해설:
- 리스트인지 판별 후 재귀 호출
- 그 외 값들은 그대로 추가
- 데이터 전처리 및 구조 평탄화 실무에서 유용
📝 문제22] 깊이 제한 있는 재귀 함수로 리스트 평탄화 제한하기
재귀 깊이를 직접 제한하여 n단계까지만 평탄화하고 그 이후는 그대로 유지하세요.
예: depth=2이면 리스트 내부의 리스트까지만 펼치고 더 깊은 구조는 남김
🖨️ 출력 결과:
[1, 2, [3, [4]]]
✅ 정답 코드:
def flatten_limit(data, depth):
result = []
for item in data:
if isinstance(item, list) and depth > 0:
result += flatten_limit(item, depth - 1)
else:
result.append(item)
return result
nested = [1, [2, [3, [4]]]]
print(flatten_limit(nested, 2))
🔍 해설:
depth파라미터를 활용해 재귀 깊이 제어- 지나치게 깊은 평탄화를 막아 구조 보존 + 유연성 확보
- 실무에서 로그, 분석 데이터 가공 시 자주 사용
📝 문제23] 재귀 호출로 중첩 리스트에서 가장 깊은 항목 추출 중첩된 리스트 중 가장 깊은 위치에 있는 최종 값을 찾아 반환하는 함수를 작성하세요.
🖨️ 출력 결과:
가장 깊은 값: 7
✅ 정답 코드:
def get_deepest(data):
if isinstance(data, list) and len(data) == 1:
return get_deepest(data[0])
return data
deep = [[[[[[7]]]]]]
print("가장 깊은 값:", get_deepest(deep))
🔍 해설:
- 재귀적으로 리스트를 한 칸씩 열어보며 가장 안쪽 값까지 도달
- 반복문으로는 구현이 어려운 구조
- 트리 구조나 JSON 탐색기 등에서 활용
📝 문제24] 중첩 리스트에서 정수 합계 구하기 다음 중첩 리스트에서 정수(int)만 찾아 합계를 출력하는 재귀 함수를 작성하세요.
🖨️ 출력 결과:
합계: 21
✅ 정답 코드:
def sum_integers(data):
total = 0
for item in data:
if isinstance(item, list):
total += sum_integers(item)
elif isinstance(item, int):
total += item
return total
nested = [1, [2, [3, "a"], 4], [5, [6]], "z"]
print("합계:", sum_integers(nested))
🔍 해설:
isinstance(item, int)조건으로 정수만 누적- 모든 깊이에 있는 값을 재귀적으로 탐색
- 실무에서 숫자 합계, 통계, 조건 기반 합산 등에 자주 응용
📝 문제25] 피보나치 수열을 메모화 없이 계산하고 호출 횟수 출력하기 재귀로 피보나치 수열을 계산할 때, 재귀 호출이 몇 번 일어나는지 함께 출력하세요.
🖨️ 출력 결과:
fib(6) = 8
총 호출 횟수: 25
✅ 정답 코드:
count = 0
def fib(n):
global count
count += 1
if n == 1 or n == 2:
return 1
return fib(n - 1) + fib(n - 2)
print("fib(6) =", fib(6))
print("총 호출 횟수:", count)
🔍 해설:
- 피보나치 재귀 구조는 중복 호출이 많음
- 호출 횟수를 통해 메모화의 필요성을 실감할 수 있음
- 실전에서는 메모이제이션 또는 반복문 방식으로 대체하는 것이 좋음
📝 문제26] 다양한 타입의 리스트 평탄화 (문자열, 숫자, 불린 포함) 다음 리스트를 재귀로 평탄화하여 한 줄로 출력하세요:
🖨️ 출력 결과:
["x", [1, ["y", False]], [[3.14], "z"]]
✅ 정답 코드:
def flatten(data):
result = []
for item in data:
if isinstance(item, list):
result += flatten(item)
else:
result.append(item)
return result
nested = ["x", [1, ["y", False]], [[3.14], "z"]]
print(flatten(nested))
🔍 해설:
isinstance(item, list)로 리스트 여부 확인 후 재귀 호출- 평탄화 결과를
+=로 병합 - 실무에서 JSON 구조, HTML 파싱, 입력 필드 전개 등에 활용됨
📝 문제27] 중첩 리스트에서 문자열의 총 길이 계산하기 중첩 리스트 안에 있는 모든 문자열의 길이의 합을 구하는 재귀 함수를 작성하세요.
🖨️ 출력 결과:
총 길이: 10
✅ 정답 코드:
def total_string_length(data):
total = 0
for item in data:
if isinstance(item, list):
total += total_string_length(item)
elif isinstance(item, str):
total += len(item)
return total
example = ["hi", ["abc", ["de", ["xyz"]]]]
print("총 길이:", total_string_length(example))
🔍 해설:
- 문자열인지 확인 후
len(item)으로 길이 누적 - 리스트이면 재귀 호출로 깊이 탐색
- 실무에서 필드 길이 제한, 문자 수 세기, 시각적 분량 계산 등에 유용
📝 문제28] 중첩 리스트에서 정수만 추출해 정렬하기 다음과 같은 리스트에서 정수만 추출하여 오름차순 정렬된 리스트로 반환하세요.
🖨️ 출력 결과:
[1, 2, 3, 4, 5]
✅ 정답 코드:
def extract_integers(data):
result = []
for item in data:
if isinstance(item, list):
result += extract_integers(item)
elif isinstance(item, int):
result.append(item)
return result
nested = [3, [1, [5, "a"], 2], "z", [4]]
numbers = extract_integers(nested)
print(sorted(numbers))
🔍 해설:
- 재귀로 정수만 수집 → 정렬은 최종 단계에서
sorted()사용 - 데이터 전처리, 분석, 검증 과정에서 활용 가능
📝 문제29] 중첩 리스트의 최대 깊이 구하기 중첩 리스트 구조에서 가장 깊은 위치까지의 중첩 깊이(depth)를 구하세요.
🖨️ 출력 결과:
최대 깊이: 4
✅ 정답 코드:
def get_depth(data):
if not isinstance(data, list):
return 0
if not data:
return 1
return 1 + max(get_depth(item) for item in data)
deep = [1, [2, [3, [4]]]]
print("최대 깊이:", get_depth(deep))
🔍 해설:
- 리스트가 아니면 깊이 0
- 리스트라면 각 항목의 깊이를 재귀적으로 조사 →
max()로 최대값 계산 - 트리 구조, JSON 문서, HTML DOM 등 분석 시 자주 사용
📝 문제30] 문자열, 정수, 리스트가 섞인 중첩 구조에서 모든 타입별 개수 세기 중첩된 리스트 안에서 다음 세 가지 타입의 요소 개수를 각각 세는 재귀 함수를 작성하세요.
- 문자열(str)
- 정수(int)
- 리스트(list, 중첩 포함)
🖨️ 출력 결과:
문자열 개수: 3
정수 개수: 4
리스트 개수: 5
✅ 정답 코드:
def count_types(data):
counts = {'str': 0, 'int': 0, 'list': 0}
if isinstance(data, list):
counts['list'] += 1
for item in data:
sub = count_types(item)
for key in counts:
counts[key] += sub[key]
elif isinstance(data, str):
counts['str'] += 1
elif isinstance(data, int):
counts['int'] += 1
return counts
nested = [1, "a", [2, ["b", [3, 4]], "c"]]
result = count_types(nested)
print("문자열 개수:", result['str'])
print("정수 개수:", result['int'])
print("리스트 개수:", result['list'])
🔍 해설:
- 각 타입별로 카운트를 저장한 딕셔너리 사용 (
counts) - 리스트일 경우 재귀 호출 + 카운트 누적
- 실무에서 데이터 구조 검사, JSON 타입 통계 분석 등에 매우 유용한 구조
